Introduction
It is an amazing time in the field of gravitational-wave astronomy—the observation of gravitational waves by the Advanced LIGO detectors from a binary black hole merger is an event of tremendous scientific significance. A century ago, Einstein developed general relativity and predicted the existence of gravitational waves. This first direct detection of gravitational waves, the so-called “GW150914” event, is a confirmation of Einstein’s theory and is the first direct observation of a pair of black holes merging to form a single black hole. The observation of GW150914, and future observations of binary black hole mergers, will provide new insights about massive black holes in the relatively nearby part of our Universe.
GW150914 will not be the only event of its type in the Universe. It can be expected that, on average, binary black hole mergers occur at some rate. When these mergers happen within a couple of billion light-years from the Earth, they will likely be directly observed by Advanced LIGO (and soon to come, Advanced Virgo). Events that are further than this will just appear as random noise in the gravitational-wave detectors (like static on an old-fashioned TV), too small to be individually directly measured. However, it will be possible to observe the sum of binary black hole mergers that have happened throughout the history of our observable Universe.
What is a gravitational-wave background?
Gravitational waves are ripples in spacetime predicted by Einstein’s theory of general relativity. Gravitational waves are produced by accelerating objects of any size, including us humans. Most of these waves, however, are far too weak to experimentally detect. In general, we can only hope to observe gravitational waves produced by the most massive objects moving close to the speed of light, such as the binary black holes that produced GW150914.
For every nearby, loud event like GW150914, there are many more that are too far away to be individually detected by Advanced LIGO. The gravitational waves from these distant binary black holes instead combine to create a relatively quiet “popcorn” background of gravitational waves. As a pair of black holes merges, it produces a short burst of gravitational waves lasting just a few tenths of a second. These mostly-quiet individual bursts are separated in time, and arrive at Earth at an average rate of about one every 15 minutes. Their exact arrival times, though, are randomly distributed, just like the random popping of individual kernels of popcorn.
A popcorn background is an example of a broader category of gravitational-wave signal called a stochastic background. In general, stochastic backgrounds are formed by the combination of many unresolvable sources. Unresolvable sources are those which we cannot distinguish individually, either because they are too quiet (as in the case of a popcorn background described above) or because there are simply too many occurring at once. Detecting a stochastic background is something like listening to voices in a crowded room. Aside from the loudest people and those standing nearest to you, you can hear the remaining conversations blend together into a continuous hum.
What can it tell us?
Gravitational waves are expected to have been created throughout the history of the Universe. Depending on when they were produced, gravitational-wave backgrounds can be classified into two basic categories: cosmological and astrophysical. Cosmological backgrounds are predicted to have been produced by sources that existed in the very early Universe just a few seconds after the Big Bang, while astrophysical backgrounds are predicted to have been produced by systems of massive stars such as the neutron stars and black holes that we see today. Most likely, contributions to the gravitational-wave background from astrophysical sources will dominate cosmological ones. The gravitational-wave signal produced by a population of binary black holes like GW150914 is an example of an astrophysical background.
The strength of the gravitational-wave background at different frequencies strongly depends on the type of sources that produce them. Thus, depending on the type of gravitational-wave background we detect, we may learn about the state of the Universe just a few moments after the Big Bang or how the Universe is evolving in more recent times. In addition, looking at whether the signal is stronger from certain directions on the sky or is uniformly spread out will give us information about the distribution of the sources that produced the background.
What does GW150914 mean for a gravitational-wave background? Why is this interesting?
GW150914 was a single event. Its gravitational waves were from the merger of two black holes, having masses of about 29 times and 36 times the mass of the Sun, forming a single black hole with a mass of about 62 times the Sun’s mass. The large component masses of the black holes making up GW150914 suggest that the unresolved popcorn signal from the population of binary black holes is probably stronger than most astrophysicists originally thought. This means we have a better chance of measuring this background with the Advanced LIGO and Virgo detectors. We will have to analyze the data for several years, but it may be possible to eventually measure the signal.
How do we detect these gravitational waves?
Although the individual signals from the binary black hole mergers have a characteristic shape, the signals from distant sources will be too weak to be individually detected and the arrival times of the popcorn-like bursts will be random. This means that the standard searches that look for single events like GW150914 won’t work for detecting the relatively quiet popcorn signal from the population of binary black hole mergers throughout the Universe. So we need to take a different approach (described below) to detect the waves from these unresolvable sources.
It is hard to search for a weak random signal using data from a single detector because the detector noise itself is also random. So instead we compare (“correlate”) data from pairs of detectors, e.g., the two LIGO detectors in Hanford, WA and Livingston, LA. The random gravitational-wave signal will be the same (“correlated”) in both detectors, while the detector noise will not (since the detectors are widely separated and most noise sources due to the environment are local to the detectors). Thus we can use this similarity (“correlation”) to distinguish the gravitational-wave signal from unwanted detector noise.
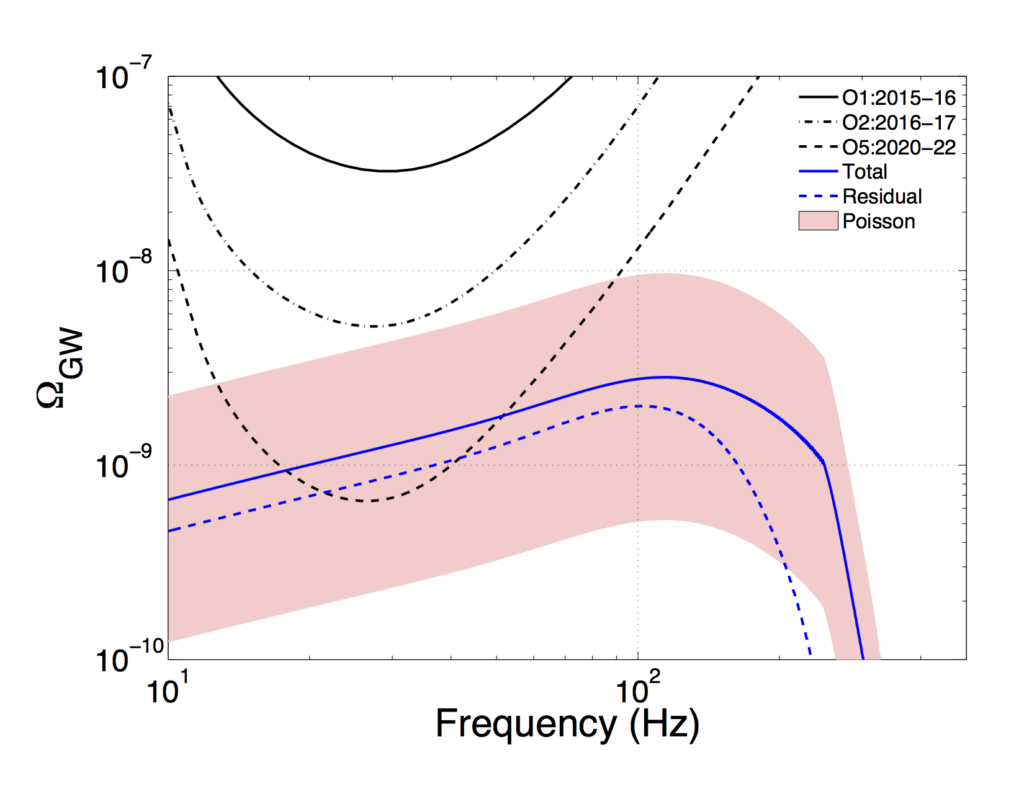
Figure 1 compares the expected strength of the gravitational-wave background for a reference model (in blue) to the expected sensitivity of the Advanced LIGO and Virgo detector networks (in black) over the next several years. The total background for all the binary black holes is the solid blue curve; the background from just the unresolvable signals is the dashed blue curve. The pink shaded region shows a range of possible signal strengths due to the uncertainty we have in the rate of the binary black hole mergers as determined from GW150914. The three black curves show how the sensitivity of the correlation search improves from the first observing run O1 to the last observing run O5, when the two advanced LIGO detectors and the advanced Virgo detector are simultaneously taking data at their peak sensitivity. (The lower a black curve is, the more sensitive the detector network.) When a blue curve intersect a black curve, as it does for O5 (dashed black curve), there is a good chance of being able to measure the correlated gravitational-wave signal relative to the detector noise.
Moreover, by performing this correlation over the whole duration of the run (which could be months or years), we build up the signal relative to the noise by including the contribution of the events that occur (on average) once every 15 minutes. The more data we have to analyze, the better it is for this type of search.
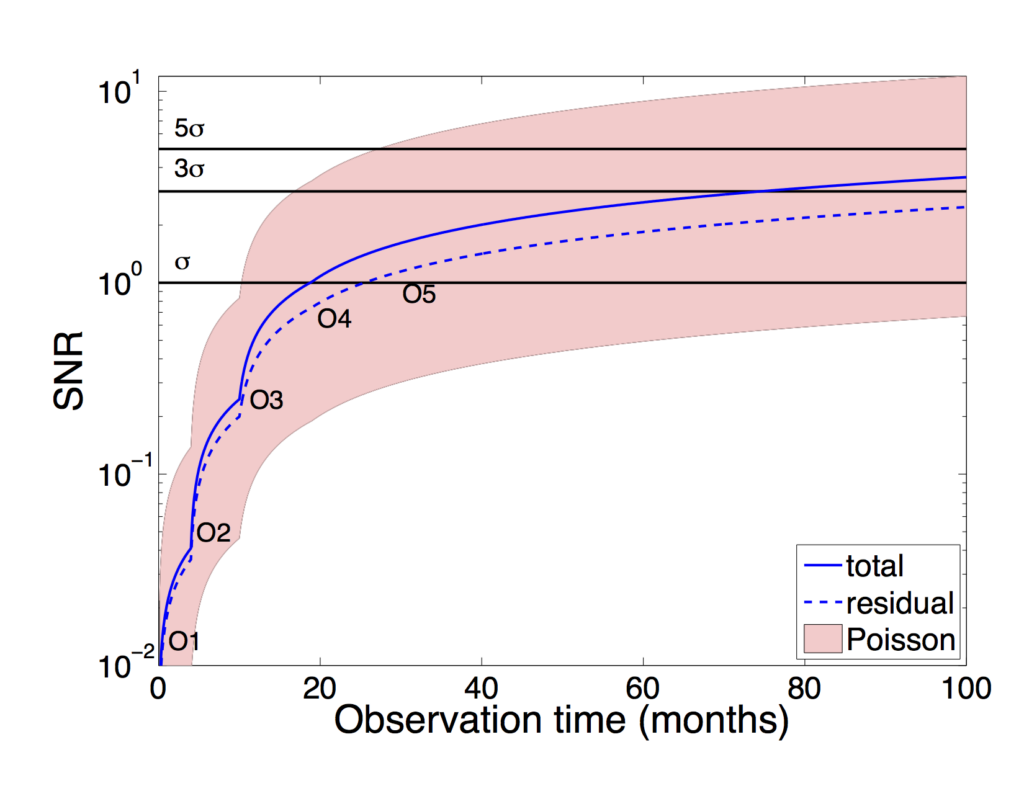
Figure 2 shows how the strength of the correlated gravitational-wave signal relative to the detector noise (called the “signal-to-noise ratio” or SNR) is expected to increase over time. (More binary black hole mergers contribute to the correlated signal when you observe for longer times.) The blue curves and the pink region have the same meaning as in Figure 1. The labels O1, O2, etc. indicate the different observing runs. The black horizontal lines correspond to different values of the expected SNR. We will be pretty confident that we’ve observed the gravitational-wave background when we measure an SNR=3 (the chance of getting such a large value of SNR from noise alone is less than 0.3%). For the reference model including all the binary black holes (the solid blue curve), this will happen in about 6 years (72 months). But if we are lucky, and the rate is at the high end of our current estimate (corresponding to the top of the pink region), then we can reach a level of SNR=3 after only 1.5 years to 2 years.
Estimating the gravitational-wave background based on what we’ve learned from GW150914
A number of factors contribute to how many binary black hole systems will form in the Universe. An important long-term research question will be to try and describe how systems like GW150914 were created. For example, maybe the two original black holes in GW150914 evolved from a binary star system, where the two stars orbiting one another were very massive. Or perhaps the system was created in a globular cluster (a group of stars tightly bound together by gravity) where one could imagine many interactions taking place that would make initially small black holes evolve into larger ones. The most massive stars are short-lived and often produce black holes upon their death, so knowing the birth rate of massive stars is important. Star formation rates depend on the amount of matter present, and its constituents; was there just hydrogen and helium present when the star was formed, or were there other elements as well? Also, how long did the two black holes take to get close enough to collide? All of these ingredients contribute to the different binary black hole formation models that we considered.
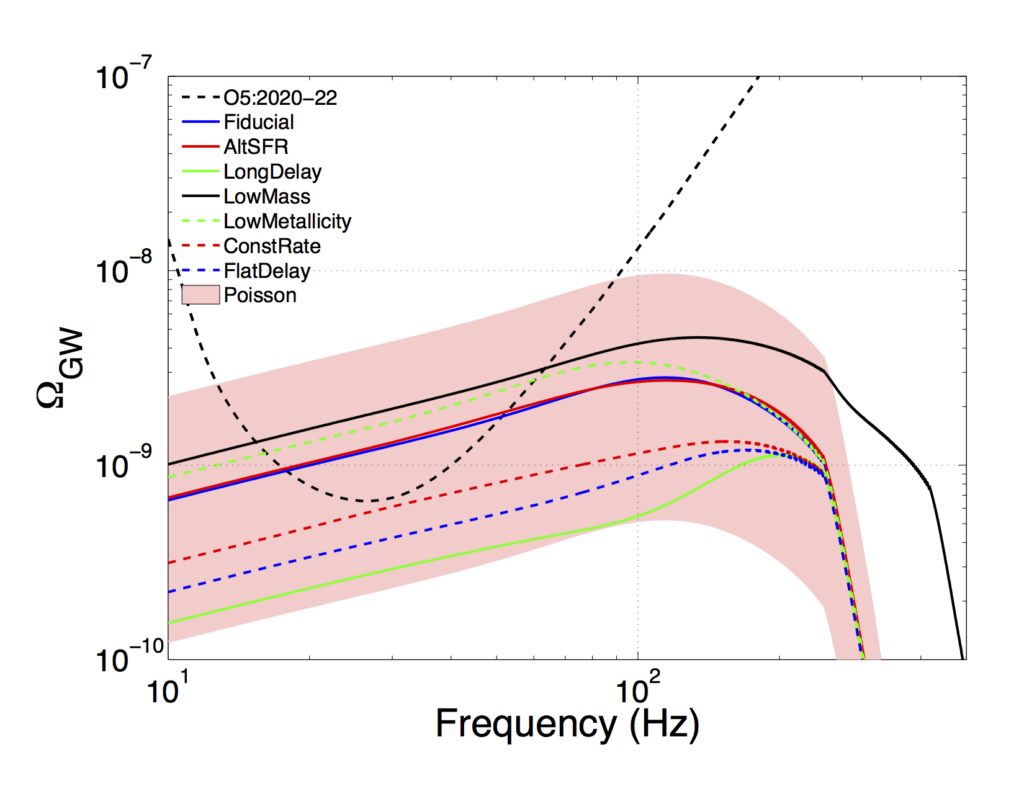
Figure 3 explores how likely we are to make a detection of the gravitational-wave background if we consider various realistic models of GW150914. The dashed black line shows the expected sensitivity of the advanced LIGO and Virgo detector network after a couple years of collecting data. The solid black line shows the prediction of the reference model and the shaded pink region shows the range of the prediction due to sizable uncertainty in our current estimate of the rate. The remaining lines show a variety of models that are consistent with what we know about GW150914. Notice that all the models fall mostly within the shaded region, meaning that we are not very sensitive to differences between the models. Also notice that the dashed black line overlaps with the shaded region, meaning there is a possibility of making a detection with the advanced LIGO and Virgo detectors.
If we detect a stochastic gravitational-wave background in the future, we will not be able to distinguish between different models describing how these binary black hole systems were created. We will, however, be able to contribute to understanding how often these mergers happen in the far away Universe. Future measurements of individual mergering black holes will provide a better estimate of how often these types of events take place in the nearby Universe and more information on the masses of the black holes. Combining what we learn from a stochastic background with measurements from individual events may help distinguish between different formation pathways for binary black holes.
Implications for the future
The GW150914 event suggests that merger rates and masses of binary black holes are on the high end of the range of earlier predictions. This means that a gravitational-wave background due to merging black holes is expected to be larger as well. There are sizable uncertainties associated with the strength of this background, but detecting it may be within reach of the advanced detectors at their peak sensitivity. Looking to the future, the next generation of gravitational-wave detectors might be able combine measurements of a gravitational-wave background with measurements of individual black hole mergers to distinguish how black holes may come to orbit one another.

