A Core-Collapse Supernova (CCSN) marks the violent death of a massive star. These explosions are some of the most spectacular events in our Universe. When a star explodes relatively close by, e.g., in our own Milky Way Galaxy, then its light can be visible even without a telescope, and a “new” star appears in the sky. Unfortunately, CCSN events are pretty rare, with approximately 2–3 occurring per century in our Galaxy. These explosions are extremely interesting, however, because all elements heavier than iron are produced in a CCSN, all four fundamental forces play a role, and the full equations of Albert Einstein’s theory of General Relativity have to be considered (although the numerical modeling is very hard and computationally expensive).
Supernovae can be observed with optical telescopes and their light gives us a lot of information about the progenitor of the explosion. However the information that we obtain from electromagnetic radiation (not just optical light, but across the entire electromagnetic spectrum) does not explain the ignition of the explosion, the so called Core-Collapse, which happens in the center of the dying star. This is a very short, violent and important phase lasting only miliseconds. In particular it is not clear how the shock wave produced can plough through the outer layers of the dying star and not lose all of its momentum. Unluckily, the light from star’s center cannot plough through the surrounding material, so from electromagnetic observations of the CCSN alone all information about the collapsing core is lost. With Gravitational Waves (GW), on the other hand, we can about learn the dynamics of the collapsing core. GWs can escape from the collapsing core, without being scattered or absorbed by the outer layers of the star, and could in principle be measured by the LIGO and Virgo GW detectors.
In our search we are analyzing interferometer data collected during four relatively close (within a distance of about 11 megaparsecs) supernova events which happened while Initial LIGO and Virgo were performing observations. Based on the electromagnetic spectrum of each supernova, the time interval of interest for searching for GWs was calculated, varying from one day to nearly two weeks. After comparing those time intervals with the GW data, only two of the CCSN events appeared to be good for further analysis. The other two had either not enough data or poor quality data during the relevant times.
In order to test the sensitivity of the GW data, and the algorithms we use for analysing the data, we injected into the data three families of artificial GW waveforms. The first set is based on fully numerical simulations of CCSN events. These signals are dominated by stochastic (i.e. random) processes, and are challenging to detect, when the CCSN is outside our galaxy. The second set of waveforms is calculated from semi-analytical calculations for models of extreme CCSN emission. In those models the GW signals have known shape and therefore are easier to detect. The last set of waveforms is created from so called “sine-gaussians“. The purpose of these signals is only to probe a specific combinations of signal frequency and time interval in relation to the CCSN – which we refer to as a specific region of the time frequency parameter space, but they can be used to constrain how much GW energy is emitted in those regions by supernovae.
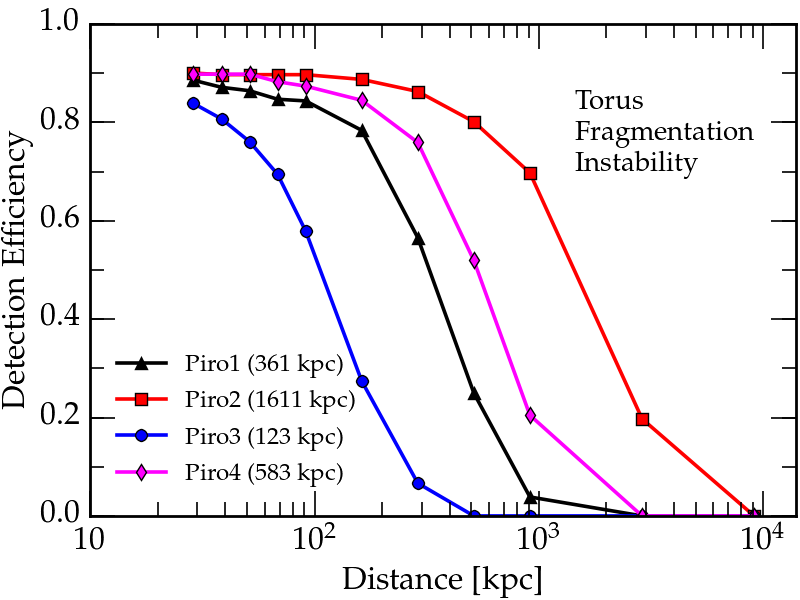
Example of the search efficiency of our algorithms with respect to distance of the CCSN, for one of the extreme emission models considered in our paper. The curves, for different model parameters, show how the probability of detecting a simulated signal decreases as the distance of the CCSN increases. The numbers in brackets show how far a CCSN would have to be before the detection efficiency drops to half of its value for a very nearby CCSN.
After the whole analysis was performed no GW were found, but we did calculate upper limits on the amount of GW energy that could have been emitted by the two supernovae. This in turn allowed us to calculate the probability with which we could exclude specific models for the emission of GWs from the supernovae. Unfortunately, in this search we cannot yet constrain or exclude any of the CCSN models considered. However, we were able to assess the future prospects for excluding these models using the upgraded Advanced LIGO and Advanced Virgo detectors.

Example of a Model Exclusion plot. The different curves show how the probability, or confidence, with which we could exclude a CCSN model is expected to scale with the sample size of observed supernovae (denoted by p) and the sensitivity to the waveform amplitude (denoted by A). Currently p=A=1 so we cannot yet make any statements excluding this model.
Read more
- A First Targeted Search for Gravitational-Wave Bursts from Core-Collapse Supernovae in Data of First-Generation Laser Interferometer Detectors Phys. Rev. D 94, 102001 (2016)
- Free arXiv preprint: arXiv:1605.01785 [gr-qc]

