Einstein’s general relativity is our most successful theory of space, time, and gravity. According to this elegant framework, the force of gravity is a manifestation of the curvature of spacetime, which is itself produced by the presence of matter or energy. In the words of legendary physicist John Wheeler, “spacetime tells matter how to move; matter tells spacetime how to curve” (source). General relativity makes many observable predictions, and so far it has passed all experimental tests with flying colors. For example, one of the key predictions of relativity is the existence of gravitational waves, which were recently detected by LIGO and Virgo.
In spite of the unquestionable success of Einstein’s theory, there are theoretical reasons to expect it will break down in some regime — for example, at extremely high energies. This means that general relativity would be unable to fully describe the physics of certain phenomena, like the singularity inside a black hole, at which point its predictions would no longer agree with observations. Observing such a discrepancy would provide invaluable information about the nature of our universe. For this reason, experimentally testing general relativity is one of the key missions of the LIGO Scientific Collaboration and Virgo Collaboration.
The sources of the observed gravitational waves are extremely fast-moving and compact objects, so they allow us to directly probe dynamic and strong gravity. LIGO and Virgo have placed some of the first observational constraints on departures from relativity in this regime. (Learn about tests of general relativity with our first detection.)
Einstein’s theory makes specific predictions about the properties of gravitational waves, but extensions to relativity need not impose these same constraints. For example, if general relativity is correct, these waves must propagate at the speed of light, but this is not required in some alternative theories. The detection of GW170817 along with gamma-ray light gave tight limits on the difference in speeds.
General relativity also predicts that gravitational waves should be come in only two polarizations, which determine the directions in which space is stretched and squeezed as the wave whizzes by. Polarizations can be understood by analogy with electromagnetic waves (light), which can be made of electric and magnetic fields oscillating in two different patterns — two polarizations. (Polarized sunglasses work by blocking one of these polarizations.)
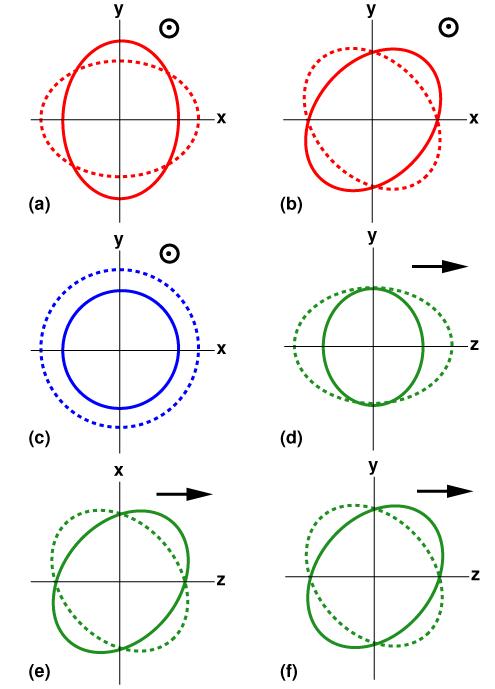
Figure 1. Representation of the six polarizations permitted in general “metric” theories of gravity. Panels (a) and (b) denote, respectively, the “+” and “×” polarizations permitted by general relativity. In these two cases, the spacetime distortion is in the plane perpendicular to the direction in which the gravitational wave travels (i.e. out of the page): an initially circular ring of particles is stretched in one direction in this plane while being squeezed in the perpendicular direction in the plane, before the pattern reverses. Panels (c) to (f) denote polarizations that are not permitted in general relativity. Panel (c) again shows a transverse polarization, while panels (d) to (f) illustrate distortions that propagate in a direction (shown by the arrow) that lies in the same plane as the spacetime distortion. (Credit: Clifford Will, Living Reviews in Relativity)
According to Einstein, gravitational waves also have two polarizations, which can be identified by the way they alternately stretch and squeeze a ring of freely falling particles in either a “+” or “×” pattern, as shown in panels (a) and (b) of Figure 1. Because of their geometric properties, the two polarizations allowed by general relativity are sometimes called “tensor polarizations.” However, alternative metric theories of gravity may allow up to six polarization patterns, including those allowed by general relativity; they are all shown in Figure 1. Evidence for the existence of any of the alternative “non-tensor” polarizations would be a direct indication of physics beyond general relativity. The detection of GW170814 gave the first experimental handle on the polarization of gravitational waves.
Along with the short-lived signals that have been detected so far, LIGO and Virgo also look for long-lived continuous waves. Rapidly spinning neutron stars, or pulsars, are one expected source of these signals. Neutron stars are the collapsed cores of massive stars that have run out of fuel. They have masses of slightly more than the Sun’s mass (∼ 2.0 × 1030 kg) packed into a sphere of radius ∼ 10 km. Those which are pulsars emit extremely regular electromagnetic pulses (usually at radio frequencies). If they have an asymmetric bump, pulsars will also emit gravitational waves, typically at twice their steady spin frequency. LIGO and Virgo regularly look for these gravitational monotones by targeting hundreds of known pulsars (learn about our standard search for continuous waves from known pulsars). The detection of a continuous wave would offer a unique opportunity to study gravitational-wave polarizations. This is because the long duration of such a signal would make it possible to distinguish the effect of the different polarizations, even with a single detector. This is generally not possible with the current network of gravitational-wave detectors and the short-lived signals detected so far.
In this study, we have for the first time looked for gravitational waves coming from a set of 200 pulsars without assuming that the signals are polarized as predicted by Einstein. This search used data from the first observing run of the Advanced LIGO detectors. As in previous studies, we have used information about these pulsars obtained through radio and gamma-ray observations, allowing us to accurately track any potential gravitational wave signal in our data over the whole length of the three-month run (a technique called “coherent integration”).
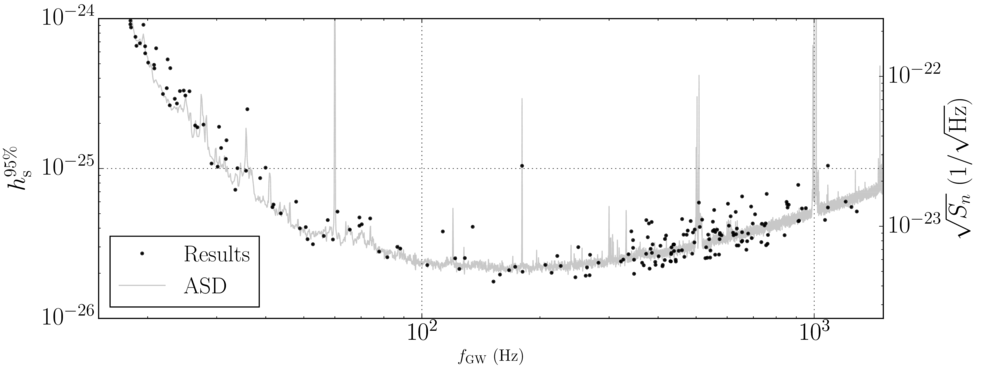
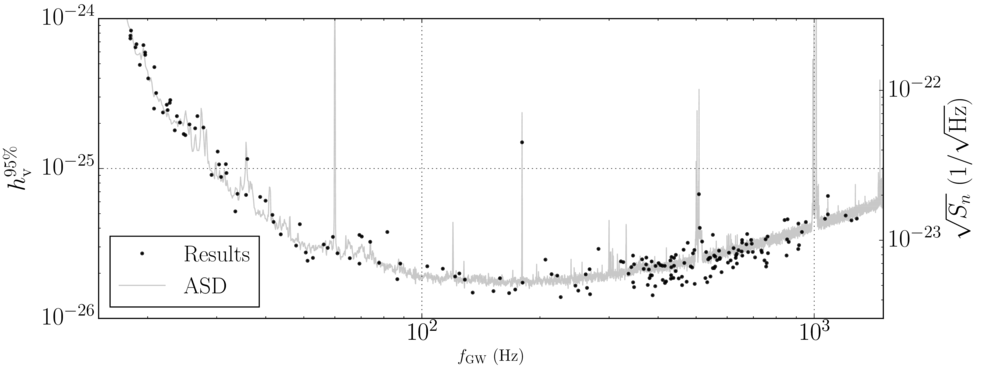

Figure 2. These plots show our upper limits on the amplitude of continuous waves as a function of the expected gravitational-wave frequency. Each dot represents one analyzed pulsar, while the lines represent the sensitivity of the detectors. The top two plots correspond to signals with non-standard polarizations, while the bottom plot corresponds to the polarizations predicted by general relativity.
While we did not detect any signals, we have produced the first upper limits for beyond-Einstein strain from any of these pulsars. This is important because, due to the nature of continuous-wave searches, previous analyses would have missed signals of nonstandard polarizations, even if they were loud. Also, these limits can, in principle, be translated into constraints on specific extensions of general relativity. With these results, we have also demonstrated the robustness of the search method, which uses rigorous statistics to allow us to look for all polarizations in an efficient way. In the future, the search will be expanded to be sensitive to signals at more frequencies.
Read more:
- Freely readable preprint of the paper describing the details of the full analysis and results: “First search for nontensorial gravitational waves from known pulsars,” by B. P. Abbott et al. (LIGO and Virgo collaborations).
- Classic review on testing Einstein’s theory: “The Confrontation between General Relativity and Experiment,” by C. Will.
- An overview article on pulsars by Michael Kramer: Pulsars, EAS Publications Series, Volume 15, 2005, pp. 219-241 (freely available preprint of the overview).
- Learn about a search for a stochastic gravitational-wave background of any polarization: “Looking for ‘Forbidden’ Polarizations in the Gravitational-Wave Background with Advanced LIGO.”

