The detected signal which comprised the first direct detection of gravitational waves lasted around two-tenths of a second. However, these short, transient signals are far from the only type of gravitational waves that can be searched for. This publication is about a search for what are known as continuous gravitational waves. Rather than the “chirp” from the first detection, imagine a faint steady tone, of constant or very slowly changing pitch (i.e., frequency), ringing continuously. This type of gravitational wave signal, known as a continuous-wave (CW) signal, can be emitted by a rapidly rotating neutron star with some form of surface asymmetry – such as a mountain on its crust, or an oscillation (called an r-mode) produced on its surface.
The search described here is called a directed search: it targets a known sky location, but searches over a wide range of star rotation speeds (or rates). In other words, it knows exactly where it’s looking, but makes as few assumptions as possible about what it might find there. In this way, the analysis has a good sensitivity to potential gravitational waves while its computational cost remains under control.
The target for this directed search is the globular cluster NGC 6544, pictured here. Globular clusters are collections of stars very tightly bound by gravity, giving them very high stellar densities – a large number of stars packed into a very small region. They are typically found in the halo of a galaxy, orbiting the galactic core. They are normally composed of very old stars, which would not be good candidates for gravitational waves because their asymmetries tend to disappear over time. However, the extremely high concentration of stars in a globular cluster could result in a high rate of interactions between stars — either with other stars or debris — which could spin a star back up and/or introduce new asymmetries. NGC 6544 is a globular cluster that is close — gravitational wave strain decreases with distance — and it has an especially high concentration of stars in its center.

Globular cluster NGC 6544. Image credit: Wikimedia.
One of the key features of this search is a new algorithm for making Doppler corrections, called barycentric resampling. A CW signal is shifted in frequency by the Doppler effect due to the motion of the Earth through space—both its daily rotation and its yearly journey around the Sun. Correcting for these Doppler shifts can be computationally intensive. The barycentric resampling method shifts each data sample in time by the light travel-time (remember that gravitational waves travel at the speed of light) between the Earth and the Solar System barycenter, which arranges the data as if it were being recorded by a detector located at the barycenter. The barycenter, unlike the Earth, does not move through space in the reference frame of our Solar System, so using this method to mimic a detector situated at the barycenter eliminates the Doppler shift and is more than ten times faster computationally. Although this search used data from the sixth initial LIGO science run (S6), this method has become standard for continuous wave searches and is already seeing extensive use in the Advanced LIGO/Virgo era.
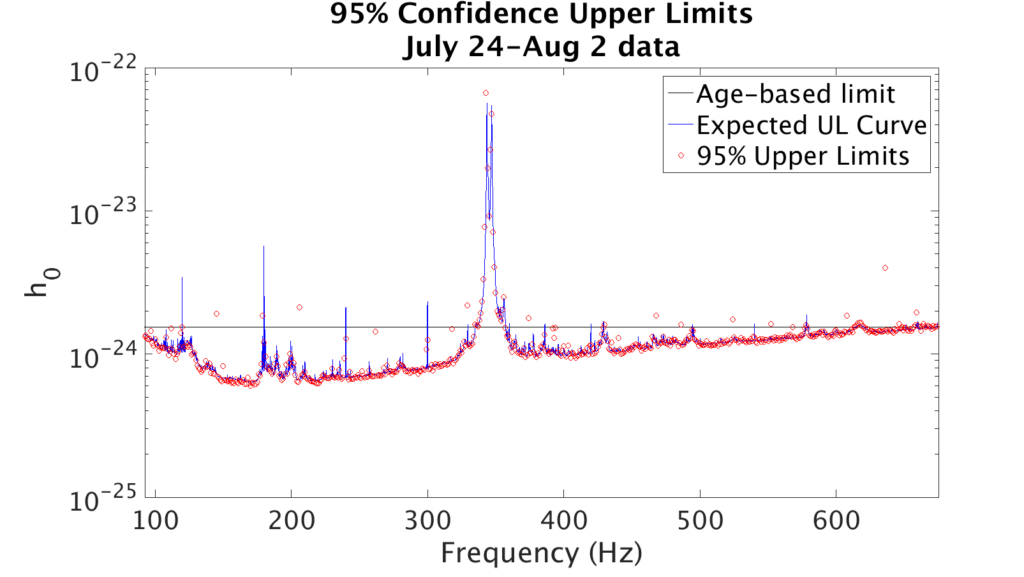
Upper limits on gravitational wave strain are the red circles. The blue curve is an expected upper limit curve calculated from the noise spectrum of our data. (A running median has been applied to the noise spectrum, which causes some discrepancies when very narrow noise artefacts are suppressed). The black line is a limit on gravitational wave strain based on energy conservation as well as the age of, and distance to, any sources in the globular cluster; it represents the loudest possible signal we could hope for.
The search found no gravitational wave signals, but was able to set what are called upper limits on the strength of possible signals. Given the sensitivity of our data, we can place a limit on the strain of gravitational waves and say that, if there had existed waves at or above the limit, our search would have detected them. These upper limits appear in Figure 2 from the paper, reproduced here. Based on energy conservation, as well as an assumed age of, and distance to, any possible sources in the globular cluster, we can set a limit on strain which represents the loudest possible signal we could see from the cluster in this search, represented by the black line. The computed upper limits lie below the loudest signal limit, which means that this analysis is scientifically relevant: it is sensitive to potentially real signals, weaker than the strongest possible one. These limits on gravitational wave strain translate into limits on the ellipticity — a measure of the spherical asymmetry — of possible neutron stars, and limits on the amplitude of the r-mode oscillations on their surfaces.

