Introduction
Gravitational waves are produced by non-uniformly accelerating masses that carry information about their sources, and are often thought of as ripples in the curvature of spacetime. Einstein’s theory of General Relativity (GR) predicts measurable properties of gravitational waves. According to GR, these waves travel at the speed of light, and the speed of propagation is independent of the frequency of the wave. It predicts the waves to have two independent modes of polarization referred to as `plus’ and ‘cross’. Further, GR makes predictions for the dynamics of spacetime that lead to the generation of gravitational waves, for instance, in the case of collisions of black holes and/or neutron stars. The gravitational-wave detections from merging binaries consisting of black holes and neutron stars by the advanced LIGO/Virgo detector network hence provide a unique opportunity to verify the predictions of GR and thereby search for any beyond-GR physics.
With the most recent gravitational wave transient catalog GWTC-3, the LIGO/Virgo detectors have detected about 90 compact binary mergers, including binary black holes, binary neutron stars, and neutron star–black hole pairs. Among the 90 events, 35 compact binary mergers from the second half of the third observing run (O3b) were reported for the first time. In this paper, we combine the new observational data with the older data to seek possible departures from GR.
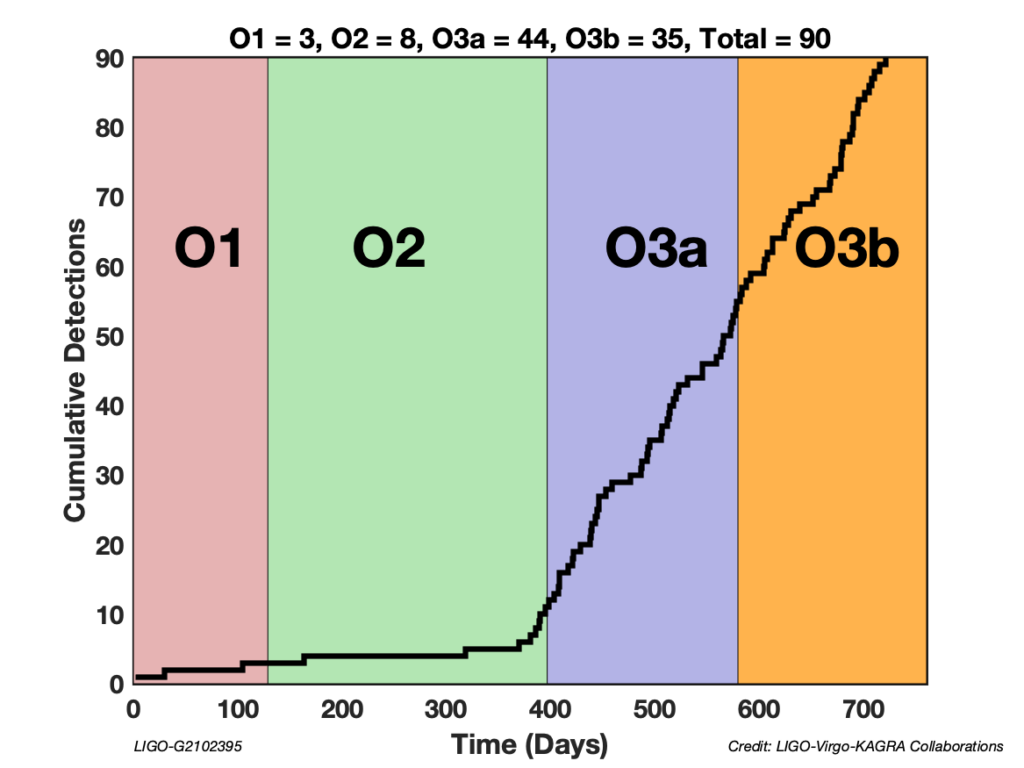
Figure 1: Durations of the first three observing runs of the advanced LIGO and advanced Virgo detectors and the cumulative number of detections made. However, as mentioned in the main text, not all of these binaries were analysed to test GR in this study.
Every experiment makes measurements in the presence of noise and gravitational wave detectors are no exception. When we search for deviations from GR, certain types of noise that are present in the detector can mimic them, creating a risk that we incorrectly claim a deviation when there isn’t any. Hence, we restrict our analysis to “loud” events only, whose signals could be expected to resemble detector noise only once in 1000 years or higher. This gives us 15 events to be analyzed from O3b and we carry out nine different tests that look for deviations from GR. A summary of the results is described below.
Consistency Tests
Overall consistency of the signal with the data: The Residual Test
We use GR waveforms to detect and interpret gravitational-wave events. The most straightforward test of GR we can perform is subtracting from the observed data the GR waveform that fits the data the best. The residual left behind by this procedure should be consistent with noise, if GR is correct. For all the events studied, we find the residual is consistent with the detector noise providing evidence for the consistency of the data with the predictions of GR.
Self-consistency of the waveform: The inspiral-merger-ringdown consistency test
Gravitational waves from mergers of neutron stars and black holes have three phases of evolution: the slow inspiral of the two bodies toward each other, the merger of the two bodies into one, and the ringdown of the remnant compact object. An important consistency check can be performed by asking whether the waveform from the inspiral is consistent with the waveform from the post-inspiral. The final mass and spin of the remnant black hole can be inferred from both parts of the evolution using empirical fits inspired by numerical relativity simulations of these binaries in GR. Our analysis found the inspiral and post-inspiral waveforms to be in good agreement for all the events that were analysed (see figure 2).
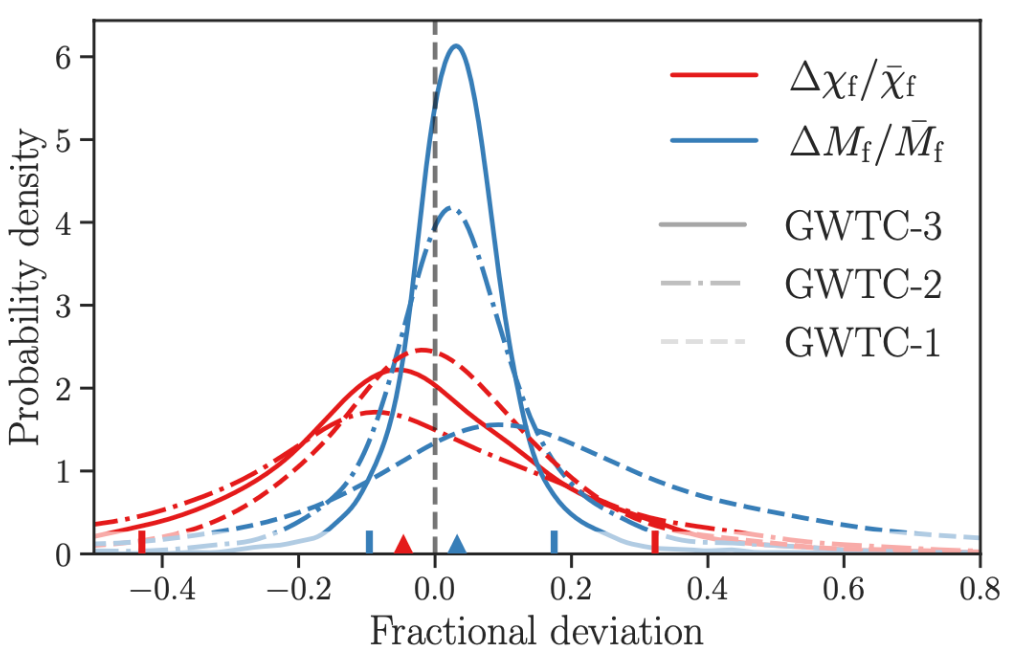
Figure 2: Fractional difference between the mass (blue) and spin (red) from the inspiral and postinspiral parts of the gravitational waveform inferred from GWTC-3 are compared against the results from the previous analyses (GWTC-1 and GWTC-2). The grey vertical line shows the GR value of zero and the results show excellent consistency with GR. (Fig. 4 of the paper).
Parameterized Tests of GR
The highly nonlinear and complex physics during the late-time dynamics of the binary leads to various physical effects that get encoded in the gravitational waveform. A modified theory of gravitation may have a different prediction for one or more of these effects. Parameterized models enable searching for possible departures from GR in these physical effects. We search for evidence of non-GR physics in the inspiral and merger/ringdown phases of the evolution.
Tests using the inspiral
The inspiral phase of the binary is described by a slow motion, weak-field approximation called the post-Newtonian approximation to GR. Different post-Newtonian coefficients capture one or more of the physical effects during the binary dynamics and testing their consistency with the GR predictions constitutes a very useful test of GR. Our analysis, combined with the results from previous catalogs, provides state-of-the-art bounds on the deviation coefficients; however, we find no statistically significant inconsistencies with GR.
The inspiral of the binary also allows us to test whether the signal is consistent with the coalescence of two Kerr black holes in GR. If one of the compact objects is spinning, this spin can result in a deformation – just like how earth’s rotation leads to flattening at the poles and bulging at the equator. This leads to a discernible contribution to the phase evolution of the binary and is different for a Kerr black hole compared to other compact objects. We test for this effect and find no evidence for any exotic compact objects.
Tests using the merger and ringdown
In a similar way, we test whether the gravitational waves emitted during merger and ringdown follow the predictions of GR. The duration of the merger and ringdown is much shorter than the inspiral, except in the case of high-mass binaries, resulting in less accumulation of signal-to-noise ratio during this part of the evolution. Restricting the events to those with reasonable signal-to-noise ratio accumulated during the merger and ringdown allows for meaningful bounds. This test is carried out with three methods that are complementary to each other in terms of the details of the waveform and methodology and parametrization. We find the test to yield consistency with GR within the statistical uncertainties.
Tests of gravitational wave propagation
While gravitational waves propagate non-dispersively according to GR, modifications to GR can lead to dispersion. This results in the frequency components of the wave traveling at different speeds, causing differences in their arrival times at the detector. For instance, if the higher-frequency waves emitted during the merger travel faster than the lower-frequency inspiral waves, then the “merger waves” might be detected earlier than anticipated We search for gravitational wave dispersion and find no evidence for it. One specific and interesting model that can be constrained here are massive graviton theories. This is a class of theories where the putative graviton particle is assumed to have a tiny (but unknown) mass. This leads to a specific type of dispersion which can be constrained providing a lower limit on the graviton mass. Based on the events analysed from all the three observing runs, the bound we obtain is that the graviton mass should be below 1.3 times 10-23 eV/c2.
Tests of gravitational wave polarization
Gravitational waves in GR can only have two states of polarization: plus and cross. However, a more general theory of gravity can have up to six different polarization modes (see figure 3). Using three detectors (the two LIGOs and Virgo), we can set a partial limit on the non-GR polarization content in the signals we observed. The method relies on constructing a stream of detector data without any GR signals. Any residuals in this detector stream would indicate the presence of additional polarization modes. Our analysis showed no such presence and the data conforms with the predictions of GR.
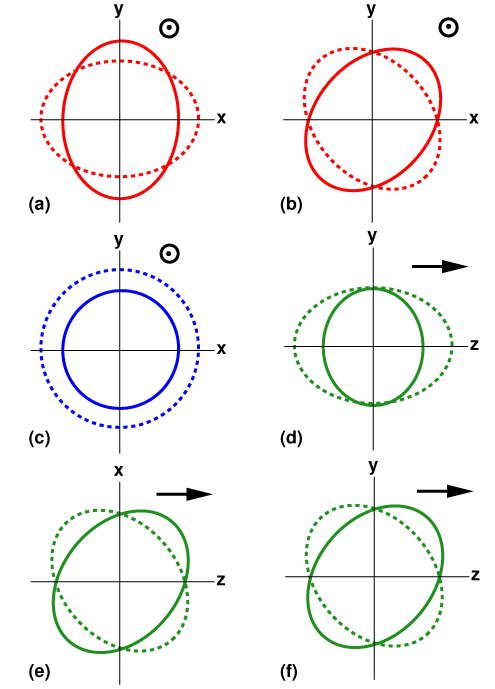
Figure 3: Representation of the six polarization modes allowed in a general gravity theory. The first three correspond to the situation when the direction of propagation of the wave is into the plane of the screen (transverse) and in the last three the arrow denotes the direction of propagation of the wave. The first two, in the top row, are the only modes allowed by GR referred to as `+’ and `x’. (Figure credit: : Clifford Will, Living Reviews in Relativity)
Post-merger Echoes
There are theoretical alternatives to black holes which are referred to as black hole mimickers, because they can mimic the properties of black holes but are not GR black holes. One of the most distinguishing properties of a black hole is the presence of an event horizon which is a surface from which nothing returns, i.e. with perfect absorptivity. However, in black hole mimickers, the equivalent of an event horizon may be a surface which, for example, may be partly or fully reflecting. It has been argued that the post-merger waveform from mergers of such objects can contain repeating echoes of the ringdown signal. We searched for such echoes in the data and found none, implying the consistency of the merger remnants with rotating black holes in GR.
Summary
We searched for evidence of possible breakdown of GR in nine different ways. We found that, within the statistical uncertainties due to noise and possible unknown systematics due to inaccurate waveform models, predictions of GR are completely consistent with the detected events. Given the importance of a detection of possible breakdowns of GR, we will keep pushing these tests in the years to come. New tests could probe entirely new facets of gravity that are not explored so far, using more sensitive detectors that will be operational in the next few years.
Find out more
- Visit our websites:
- Read a free preprint of the full scientific article here or on arXiv.org.

