Black hole spectroscopy and tests of general relativity with GW250114

Detecting the GW250114 signal

On January 14, 2025, the LIGO-Virgo-KAGRA collaboration observed an exceptionally loud gravitational-wave signal, named GW250114. The signal was recorded by the LIGO detectors in Hanford, Washington, and Livingston, Louisiana, during the second segment of the fourth LIGO-Virgo-KAGRA observing run (O4b).

Figure 1.  Visualization of the GW250114 post-merger black hole, showing an artistic representation of the gravitational waves produced during the ringdown phase:  as the newly formed black hole is settling into a stable state it emits gravitational waves at a set of specific frequencies like the distinct tones of a ringing bell. [Image credit: LIGO Scientific Collaboration/Sonoma State University/A. Simmonet]

GW250114 stands out as the clearest gravitational-wave signal observed so far, about three times louder than the first detection in 2015. Here, “louder” refers to its higher signal-to-noise ratio, a measure of how clearly the gravitational waves rise above the detectors’ background noise. The signal matches what is expected when two black holes of nearly equal mass and low spin spiral together, collide, and settle into a single, larger black hole.

Another article recently published in Physical Review Letters reports the detection of GW250114, presenting the properties of the black holes and a select set of fundamental physics tests. This article serves as a companion study, focusing on black hole spectroscopy and precision tests of general relativity.

Testing Einstein’s theory with GW250114

Because of its exceptional loudness, GW250114 provides an unparalleled opportunity to test whether Albert Einstein’s theory of general relativity still holds in the most extreme conditions known: the rapidly changing, intense gravitational fields near merging black holes. The goal of these tests is to check whether the observed gravitational-wave signal is fully consistent with Einstein’s predictions, or whether any deviation might hint at new physics beyond general relativity.

One of the key tools for this is called black hole spectroscopy. This technique focuses on the ringdown – the phase just after the merger when the newly formed black hole is settling into a stable state – by studying the distinct tones it emits. Much like a struck bell that rings at distinct tones, a newly formed black hole emits gravitational waves in a set of characteristic quasinormal modes.

According to the no-hair theorem, a black hole in general relativity is completely described by its mass, spin, and electromagnetic charge. In astrophysical environments, however, any significant charge is expected to be neutralized very quickly, leaving mass and spin as the only relevant quantities. This means that the frequencies of the quasinormal modes and how quickly each fades are uniquely fixed by those two numbers.

Detecting multiple ringdown tones, and checking whether they are consistent with the expected frequencies and decay times, provides a powerful test of general relativity. Such measurements not only probe the no-hair theorem, but also allow searches for generic deviations from Einstein’s predictions, whether arising from exotic black-hole features or more fundamental modifications to the theory of gravity.

In general relativity, the unique solution describing an astrophysical rotating black hole is the Kerr metric. Our spectroscopy measurements therefore test whether the remnant formed in GW250114 is consistent with a Kerr black hole, and within current precision its properties do indeed align with this expectation.

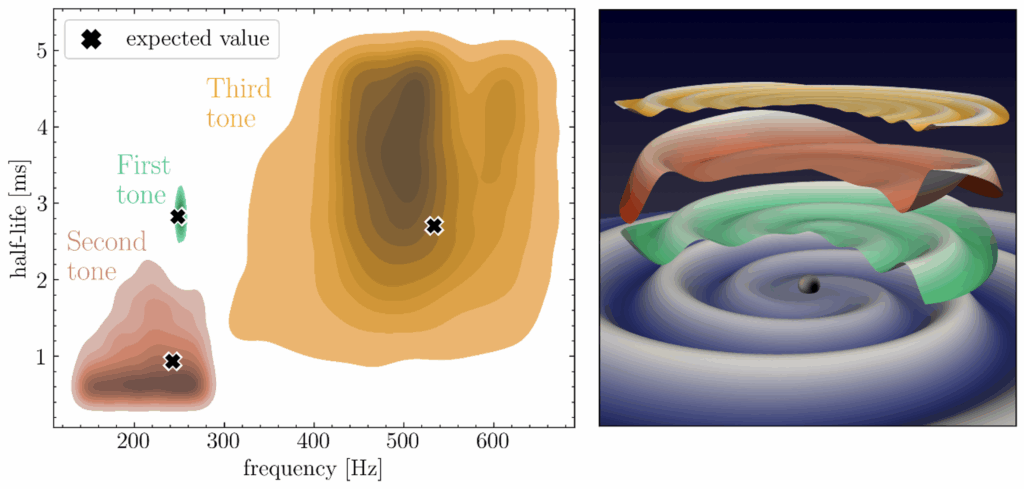
Figure 2. Left panel: Frequency and decay time (half-life) of the different ringdown tones identified or constrained in GW250114. The colored regions show results from analyses that allow the quasinormal-mode frequencies and decay times to vary freely. The red region corresponds to the overtone detected in the ringdown-only analysis (second tone), while the green and yellow regions correspond to the fundamental (first tone) and higher-frequency secondary tone (third tone)  obtained from the full-signal analysis. The black markers indicate the values predicted for a Kerr black hole with the mass and spin inferred from the full-signal analysis assuming general relativity. The shading denotes probability regions, from 90% (lightest) to 10% (darkest). Right panel: Decomposition of the gravitational-wave signal (bottom spiral, in blue) emitted by the remnant black hole (bottom sphere) into the different tones, for a numerical simulation matching the measured parameters of GW250114. The green, red, and yellow surfaces correspond to the first (fundamental), second (overtone), and third tones, respectively.

Listening to the ringdown: fundamental tone, overtone, and a higher-frequency secondary tone

Using ringdown-only analyses, which focus solely on the part of the signal after the merger, we look for these tones without using any information from the earlier inspiral. We find that the data favor a description with the main fundamental tone and its first overtone, which is a faster-fading version of the same vibration. The first overtone can be tracked for about three milliseconds after the merger, after which it can no longer be resolved above detector noise. Its measured amplitude and phase agree with detailed numerical-relativity simulations of black-hole mergers in general relativity. The tones’ frequencies and decay times are found to be consistent with theoretical predictions within measurement uncertainties. The overtone measurement is shown in Figure 2 (red shading), alongside the black marker that indicates the value expected for a Kerr black hole with the mass and spin estimated from a full-signal analysis under the assumption of general relativity.

We also analyze the full signal – including the inspiral, merger, and ringdown – with models calibrated to numerical simulations, but allowing the tones’ frequencies and decay times to vary freely, rather than fixing them to the Kerr prediction. By incorporating information from the entire signal, we can measure the ringdown’s properties even more precisely. With this method, the fundamental tone’s frequency is measured to about two-percent precision, and its decay time to about nine percent, both in excellent agreement with general relativity. This analysis also provides the first constraints on a higher-frequency secondary tone, which rings at roughly twice the frequency of the fundamental, once again matching theoretical predictions. Both of these results are shown in Fig. 2, where the fundamental and secondary tones appear in green and yellow shading, respectively.

Together, the ringdown-only and full-signal analyses offer complementary tests, confirming that the remnant’s properties are consistent with those expected for a Kerr black hole when measured in different ways.

Consistency across the inspiral–merger–ringdown signal

We also test general relativity’s predictions for other parts of the signal, beyond the ringdown. In the early inspiral phase, where the black holes orbit each other more slowly than in the final merger, we find no evidence for departures from Einstein’s predictions. We also compare the mass and spin of the final black hole estimated from the early part of the signal with those inferred from the later merger and ringdown, again finding agreement.

Remarkably, the strength of GW250114 allows us to place constraints on possible deviations from general relativity that are not only comparable to, but in some cases two to three times more stringent than those obtained by combining information from dozens of signals in the latest fourth Gravitational-Wave Transient Catalog (GWTC-4.0), which includes signals up to the first segment of the fourth LIGO-Virgo-KAGRA observing run (O4a). Some of these improvements are illustrated in Figure 3.

Finally, we check whether subtracting the best possible general-relativity waveform from the data leaves behind any unexplained pattern. It does not, and the leftover signal behaves like ordinary detector noise.

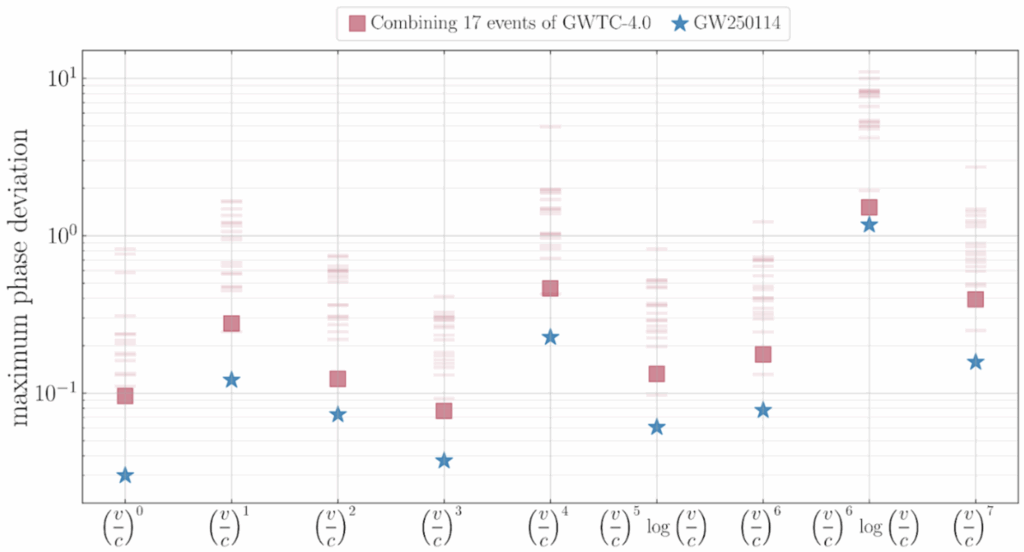
Figure 3.  Measured 90% upper bounds on possible deviations from general relativity in the post-Newtonian expansion of the inspiral phase of the gravitational-wave signal. The post-Newtonian framework describes the inspiral phase as a series in powers of the binary’s orbital velocity (v/c), where c is the speed of light, with each coefficient predicted uniquely by general relativity. For the (v/c)¹ term, general relativity predicts the coefficient to be exactly zero, so the bound corresponds to an absolute deviation; for all other orders, bounds represent fractional deviations. The blue stars show the constraints measured from GW250114. For comparison, light red bands mark results from individual GWTC-4.0 signals, and red squares indicate combined catalog constraints from 17 events. Across all post-Newtonian orders, the measurements from GW250114 place upper bounds that are two to three times more stringent than those obtained by combining multiple events.

Einstein holds firm

In every test, GW250114 matches the expectations of general relativity, within the precision of current observations. The strength and clarity of this signal make it the most precise confirmation yet of Einstein’s theory for black hole mergers, significantly tightening the limits on how much any alternative theory of gravity could differ from it. Together with the detection paper, which tests Hawking’s area law and provides complementary results on the Kerr nature of the remnant, this study illustrates the breadth of science unlocked by GW250114.

As the LIGO‑Virgo‑KAGRA collaboration celebrates a decade since the first detection of gravitational waves from merging black holes, dramatic improvements in detector sensitivity now allow us to record signals such as GW250114 with unprecedented clarity. Each new advance promises even louder signals in the future. GW250114 is therefore a preview of the transformative science that upcoming observing runs will enable: stronger detections will reveal black‑hole properties in finer detail and push Einstein’s theory to its ultimate limits.

Find out more:

Back to the overview of science summaries.