The effort to observe gravitational waves was crowned with success in September 2015 when LIGO detected a signal emitted by the coalescence, and subsequent collision, of a pair of black holes. More gravitational wave events have since been observed by the Advanced LIGO and Advanced Virgo detectors. To date, 10 binary black holes mergers and one binary neutron star merger have been found in data from the first observing runs (O1 and O2) of the Advanced LIGO and Advanced Virgo observatories. In addition to these transient signals, characterized by time durations ranging from a fraction of a second to tens of seconds, sources of continuous quasi-sinusoidal gravitational-wave signals are also expected to exist and are subject to intense research. In this paper we describe the results of an analysis aimed at searching the whole sky for continuous gravitational waves emitted by isolated rotating neutron stars, which are among the most prominent sources of this kind.
Neutron stars, the remnants of supernova explosions of massive progenitor stars, are extremely compact objects, with masses similar to that of our Sun compressed into a sphere with radius of about 10km. They can spin up to several hundred times per second. A neutron star can emit continuous gravitational waves, with a frequency twice the star’s rotational frequency, if it possesses an asymmetry with respect to its rotational axis, e.g. if it has a “mountain” on its surface, or it is slightly non-spherical. According to current theoretical models, a mountain on a neutron star would be at most just a few centimeters high, and could result from the turbulent environment characterizing a new born neutron star, frozen in the crust as it cools down in the first few seconds after its birth. Other global deformations can also occur, for instance as a consequence of a strong inner magnetic field.
Regardless of its origin, the size of any asymmetry on the neutron star dictates the star’s “ellipticity”. Ellipticity is an important quantity as the gravitational wave signal amplitude increases linearly with it, i.e. the bigger the asymmetry or bump, the bigger the gravitational wave it will generate. A bump of a few centimeters corresponds to an ellipticity of few times × 10-6. Determining a neutron star’s ellipticity is very difficult. How high a mountain can be before it collapses under the extreme gravity of a neutron star depends on the properties of the matter of which the star is composed. The deformation induced by the magnetic field also depends on the properties of high density matter, on the strength of the magnetic field and also its configuration. All these variables are poorly known.
Roughly 2500 neutron stars are currently observable by their emission of electromagnetic radiation (EM) mainly in the radio, gamma-ray and X-ray frequencies. Astronomers can detect these neutron stars because a “beam” of EM radiation happens to sweep past the Earth as the star rotates (like a lighthouse beam becoming visible when it sweeps past your eyes). But astronomers estimate that as many as 100 million or more neutron stars actually exist in the Milky Way. Most are not visible through EM radiation because they are either too faint or their beams of emission are not pointed toward Earth (we never ‘see’ it). However, if any of these neutron stars have asymmetries, they may emit gravitational waves detectable by today’s advanced gravitational-wave detectors. Our search was designed to detect signals from these objects.
Detecting such signals buried in the data is difficult. The signal emitted by an asymmetric spinning neutron star is basically sinusoidal, but many factors modify the signal received at the detector. For one, the Doppler effect, caused by the detector’s motion as the Earth rotates on its axis and revolves around the Sun, shifts the signal frequency over time. This frequency modulation depends on the relative positions of the source and the detector, on the neutron star rotation frequency itself, on the time of the day and even on the day of the year (i.e. where the Earth is in orbit around the Sun). To complicate matters further, a neutron star loses rotational energy through the emission of gravitational waves and electromagnetic radiation, causing a gradual decrease of the signal frequency called spin-down.
Given a set of possible parameters of the source, namely the position in the sky, the spin frequency and the spin-down rate, an emitted waveform can be predicted by theory. But without knowing the spin frequency, the spin-down rate and sky position, an enormous number of signal waveforms is possible, making such search extremely complex and computationally demanding. It is therefore only feasible by employing hierarchical methods. Hierarchical search methods are less sensitive than the optimal procedure, which is based on “matched filtering”. Matched filtering is used to search for the transient signals emitted by merging binary systems), but it requires precise knowledge of the source parameters. It relies on our ability to closely and with extreme accuracy follow the faint signal as it evolves during its time in the detectors. Doing so maximizes the collected signal energy, which increases with the observing time, with respect to that due to the detector noise. Unlike matched filtering, hierarchical methods model the signal evolution less accurately. This makes the search less sensitive but more robust with respect to signal model uncertainties, and feasible from the computational point of view, despite the full lack of information on the neutron star parameters.
Using hierarchical methods, the entire data set is broken into segments of time ranging from about 30 minutes to about six days (this is much longer than transient signals duration). Each segment is then independently analyzed and the information from the different segments is combined into a “detection statistic” (a number for each set of searched parameter values). This is used to estimate how compatible our result is with an assumption that the data consist of noise only (i.e. no gravitational wave signal is present). If, for a given set of parameters, the detection statistic is not compatible with the noise hypothesis, then a more refined search around that set of values is done in order to confirm or reject it as a gravitational wave candidate.
A major complication with this method is that detector data typically contain several disturbances which may look like (though they are not) gravitational wave candidates. These are called “spectral lines” as they appear as narrow peaks at a given frequency. An important part of this analysis, therefore, is identifying such noise artifacts and vetoing them, which excludes them from further study.
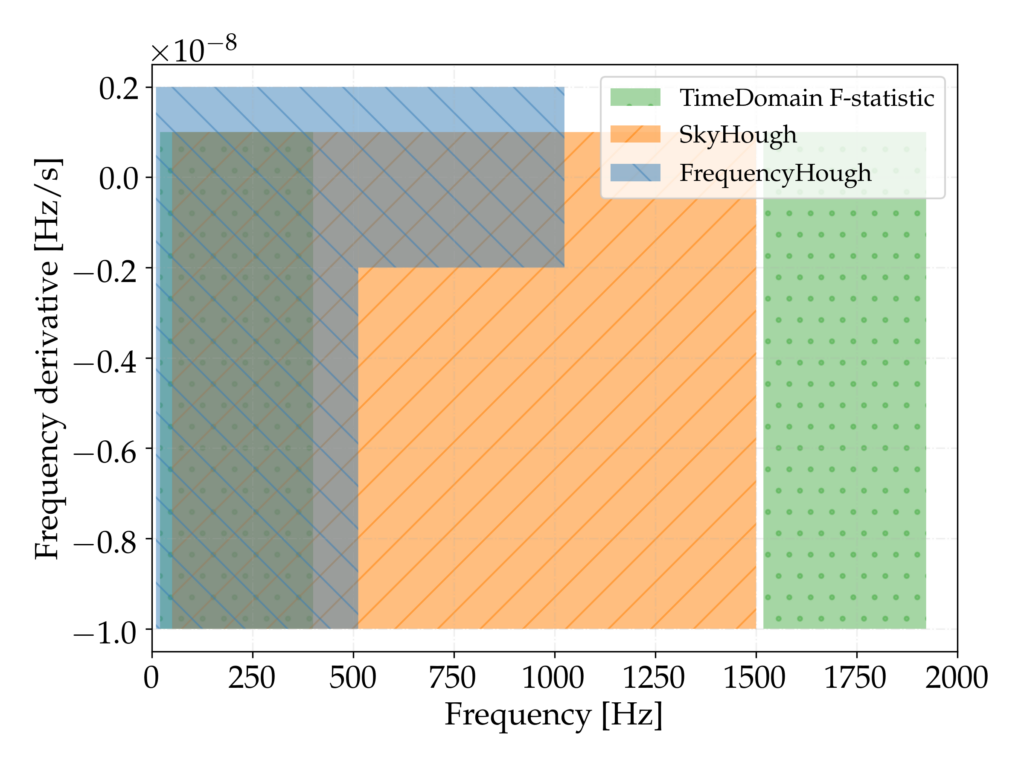
Figure 1: Each search covers a different portion of the parameter space, with some overlapping.
The sensitivity reached by the Advanced interferometers detectors during O2, which lasted for about 9 months, enabled the most sensitive all-sky search ever done in a source parameter space consisting of the whole sky, emission frequencies between 20 Hz and 1922Hz and a spin-down range from -1.0 × 10-8 Hz/s to 2.0 × 10-9 Hz/s. Our publication describes the results of this search performed with three independent hierarchical methods, called FrequencyHough, SkyHough, and TimeDomainFstat. Each method covered a different portion of the parameter space, as shown in Figure 1, used different lengths of time for the data segments, applied different data cleaning procedures to reduce the impact of noise in the data, and used different techniques to follow-up possible candidates.
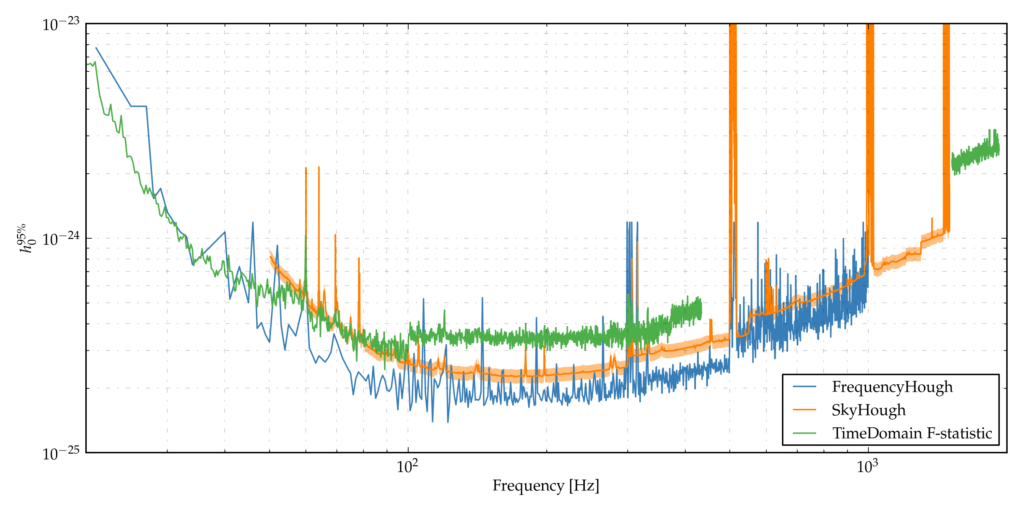
Figure 2: Upper limits on signal amplitude as a function of the frequency. The different symbols/colors correspond to the upper limits computed by the three different analysis methods.
Our analyses did not find any evidence of continuous-wave signals in the data. However, we have computed upper limits on the signal amplitude, i.e., limits on how strong a signal could be and not be detected (Figure 2). For instance, at a frequency of about 150 Hz we can exclude the presence of signals with gravitational-wave strain amplitude of ~ 1.7 × 10-25 or higher with a 95% confidence level. Figure 3 shows the so-called “astrophysical reach” of the search, which is the relation between the frequency, spin-down and distance of a potentially detectable source. As an example, a source with an ellipticity larger than roughly 2 × 10-7 emitting a signal at 1000 Hz or larger would have been detectable in our analyses if it was closer than 1000 parsecs and if the gravitational-wave-induced spin-down was larger, in modulus, than about 5 × 10-10 Hz/s.
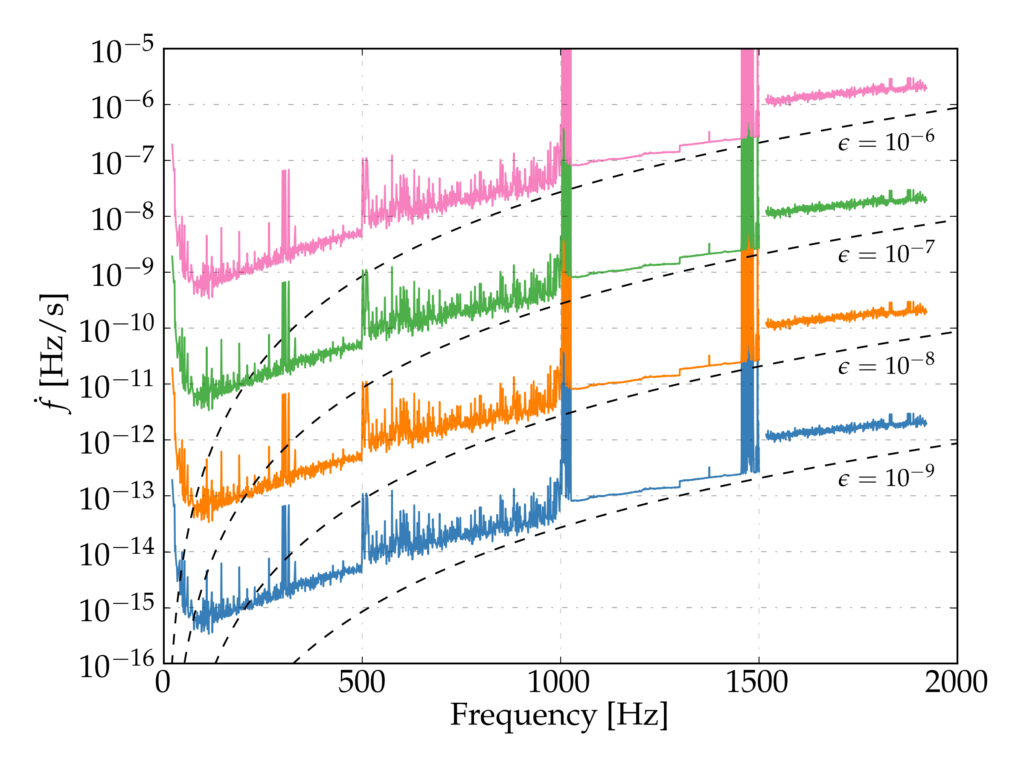
Figure 3: The astrophysical reach of the search shown here is a relation between the frequency derivative and the frequency of a gravitational-wave signal emitted by a detectable source placed at various distances. Going from the bottom to the top, the four curves correspond to a distance of 10 parsecs, 100 parsecs, 1000 parsecs, and 10,000 parsecs respectively. The dashed lines represent lines of constant ellipticity. In our analyses, a source with an ellipticity larger than roughly 5 × 10-7 and emitting a signal at 500 Hz would be detectable in our analyses at distances below about 1000 parsecs if its gravitational-wave-induced spin-down was larger, in modulus, than about 5 × 10-11 Hz/s.
Results presented in this paper constitute a significant improvement, in terms of upper limits, compared to previous analyses over a large portion of the parameter space (see, e.g. here). Although no detection can be claimed, our results are nevertheless interesting from the astrophysical point of view and shed some light on the properties of galactic neutron stars. For one, it appears that we can exclude the presence of nearby (say, within 100 parsecs from the Earth) fast spinning neutron stars with ellipticity as low as 10-8, which is just 1/100th the maximum value such objects could possess, according to current models.
As the Advanced LIGO and Advanced Virgo detectors increase in sensitivity, and other detectors join the ground-based network, we will both be able to detect gravitational waves from smaller star deformations, and probe a larger portion of the Galaxy. Hence, the probability of detecting continuous gravitational-wave signals emitted by rapidly rotating neutron stars will significantly increase. The detection of these signals will open a new frontier in the study of these fascinating compact objects, which will become true laboratories for astrophysics and fundamental physics, enabling accurate studies on the star characteristics and internal structure. Indeed, persistence is a key feature which distinguishes continuous gravitational wave signals from transient ones: once a source is detected, it can monitored for arbitrarily long times. This allows us to increase the detection confidence to almost absolute certainty and to measure the star parameters with extremely high accuracy, providing a wealth of information that would be impossible to obtain in other ways.
Read more:
- Freely readable preprint of the paper describing the details of the full analysis and results: All-sky search for continuous gravitational waves from isolated neutron stars using Advanced LIGO O2 data by B. P. Abbott, et al.

