Introduction
The Universe is expanding and steadily cooling down. This process may lead to the creation of cosmic strings: these are one-dimensional topological defects, the energy of which is concentrated along a line. Cosmic strings are analogous to the cracks which can appear in ice as the water freezes. In the Universe, cosmic strings are generally curved, they evolve, and they may form closed loops as the result of their interactions.
Cosmic strings exist in many field theories motivated by particle physics and there are several observational predictions that can be made about them. This means that cosmic strings could provide us with a tool for probing physics beyond the Standard Model, at energy scales much higher than those reached by accelerators like the Large Hadron Collider at CERN. In particular, the production of gravitational-wave signals by cosmic string is one of the most promising observational signatures that we can search for with ground-based detectors like LIGO, Virgo and KAGRA.
Gravitational Waves from Cosmic String Loops
Cosmic string loops oscillate and radiate energy, mainly in gravitational waves, which causes them to shrink and eventually decay. The gravitational-wave spectrum of an oscillating loop is dominated by string features called cusps and kinks. The former are points on the string that briefly travel at the speed of light; the latter are discontinuities which appear in pairs as the result of strings exchanging partners. Many of these gravitational-wave bursts can add together, forming a stochastic (i.e. randomly determined) gravitational-wave background. Occasionally, sharp high-amplitude bursts may stand above the stochastic background — like the shout of a lone voice heard above the sound of a noisy crowd — and so could in principle be detected individually.
We searched for gravitational-wave signals produced by cusps, kinks and kink-kink collisions (see Figure 1) in the data collected by the Advanced LIGO and Advanced Virgo detectors during their third Observing Run, denoted O3. We considered two analytic models (called A and B) for how cosmic string loops are distributed, based on the results of two different computer simulations of this distribution. In addition, we developed a third model (called C) which was designed to be more “agnostic“ by interpolating between models A and B; in our search we considered two variants (C-1 and C-2) of that model.
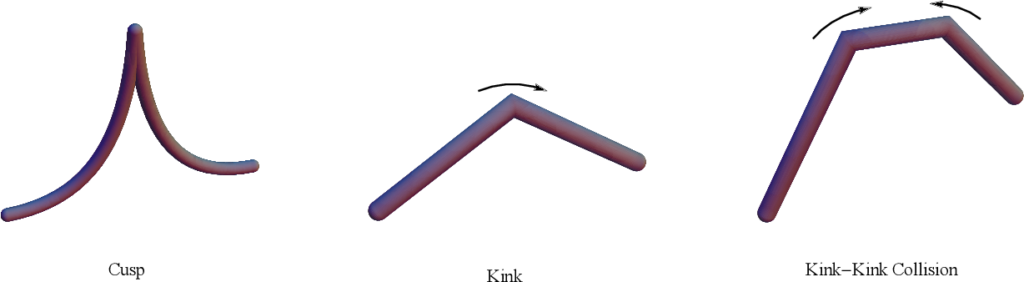
Figure 1: Illustrations of cusps, kinks and kink-kink collisions. [Image credit: Long, Hyde and Vachaspati]
Analysis and Results
We used LIGO and Virgo detector data to analyse, in each of these four models, the possibility of both a gravitational-wave burst signal from an individual cosmic string and a stochastic background of cosmic string signals. To carry out our burst search, candidates that matched the predicted gravitational waveform for such a signal were first identified and then further analysis methods were used to calculate the likelihood that each candidate event was a cosmic string signal rather than detector noise. The stochastic background search was carried out by computing the energy density of cosmic string gravitational-wave signals predicted in each of the models that we considered; these predictions were then compared to detector observational results that use the absence of a signal to place upper limits on this energy density.
Although we did not detect any cosmic string signals, our analysis allowed us to constrain the two cosmic string parameters, the string tension and the number of kinks per loop, for each of the loop distribution models — in order that the values of these parameters were consistent with our non-detection. These constraints are shown in Figures 2 and 3. In particular, we have found that the tightest constraints on the string tension come from our analysis of the search for a stochastic gravitational-wave background.
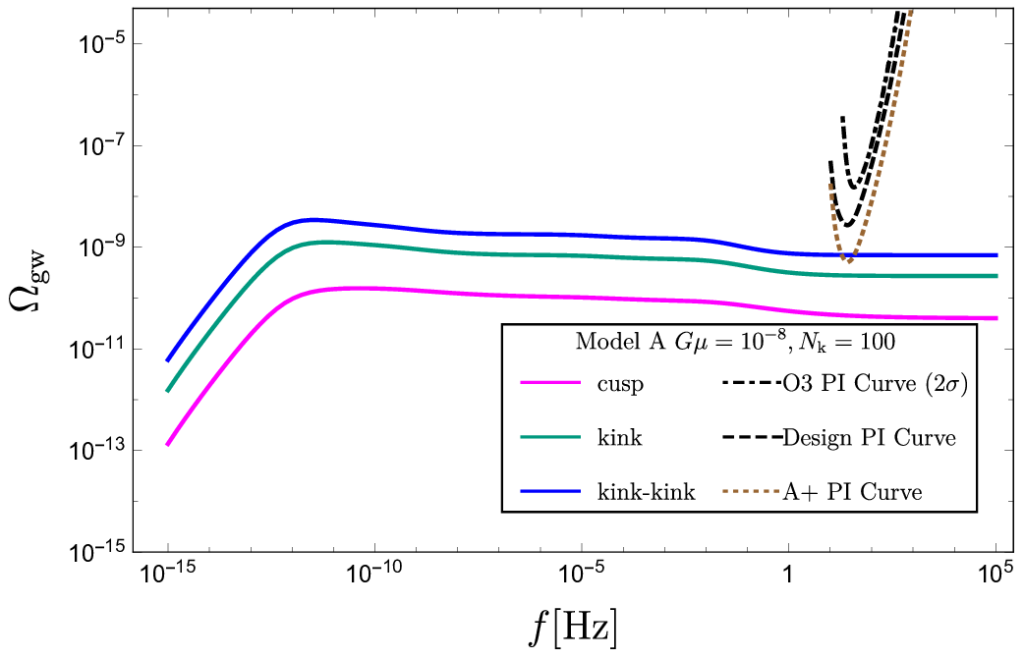
Figure 2: Predictions of the gravitational-wave energy density spectra using different models (called, A, B, C-1) for the loop distribution function and varying the number of kinks per loop oscillation, Nk. The string tension Gµ is fixed to 10−8. Note that G stands for Newton’s constant and µ denotes the string linear mass density. Top-left: model A, Nk = 100. Top-right: model B, Nk = 100. Bottom-left: model C-1, Nk = 1. Bottom-right: model C-1, Nk = 100. We also show the energy density spectra of the three different components and 2-σ power-law integrated curves for the O3 isotropic stochastic search and projections of those curves for the network of LIGO Hanford, LIGO Livingston and Virgo at their design sensitivity, and for the Advanced LIGO+ (A+) detectors. You can click on the individual panels for larger versions.
We have also compared our results with limits obtained from pulsar timing array measurements, and indirect limits from Big Bang nucleosynthesis and observations of the cosmic microwave background. The next observing run, O4, will give us a new opportunity to search for gravitational-wave signals from cosmic strings, as the LIGO and Virgo detectors are made even more sensitive and the KAGRA detector joins the global network.
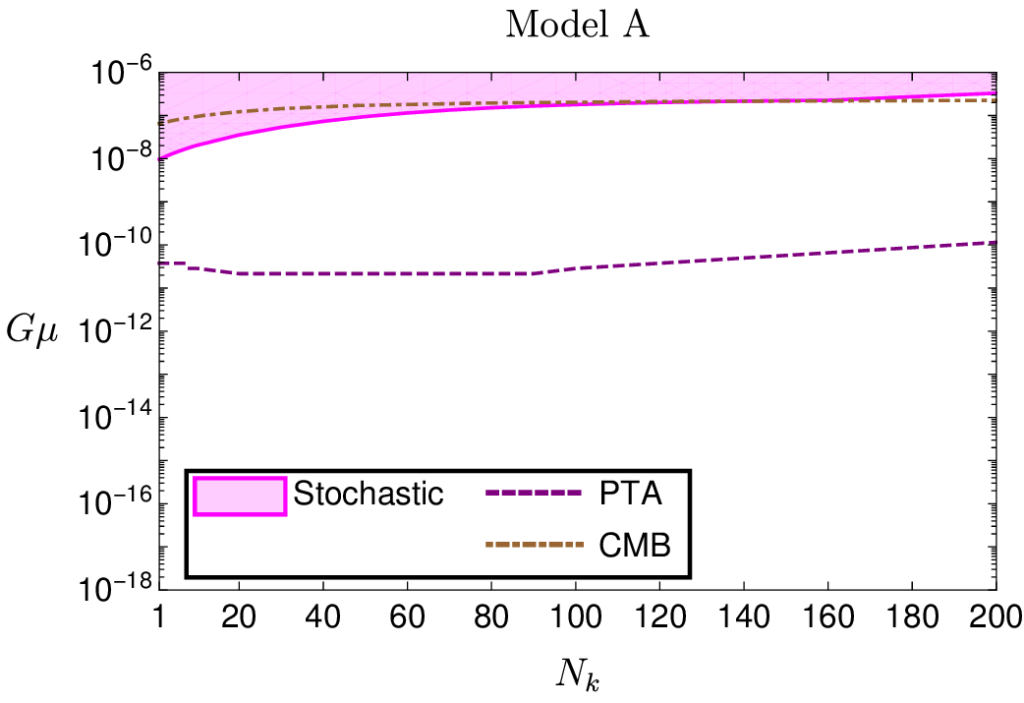
Figure 3: Advanced LIGO-Virgo exclusion contours, at 95% confidence levels, on the cosmic string parameter space, (Nk; Gµ), derived from the stochastic search (pink), the burst search (light green) and both searches (dark green). The contours indicate regions of the parameter space within which we are 95% confident that the true parameters are not found. Four models are considered to describe the distribution of cosmic string loops: model A (top-left), model B (top-right), model C-1 (bottom-left) and model C-2 (bottom-right). Note that the results from the stochastic search combine the data from observing runs O1, O2 and O3 while the burst search only includes O3 data. You can click on the individual panels for larger versions.

