Neutron stars are remnants of supernovae, the explosions of massive stars, and they are the densest objects in the universe after black holes. They have a mass of 1.4 times the mass of our sun or more, but a radius of only about 10 km! They have magnetic fields that can be between one hundred million and one quadrillion (one million times one billion) times stronger than the Earth’s magnetic field. As the neutron star rotates, it emits electromagnetic waves (such as radio waves or X-rays) out of its magnetic poles and with telescopes sensitive to those wavelengths (see X-ray and radio telescopes), we can see pulses of those waves on Earth as they sweep by us like a lighthouse (see Figure 1). We call neutron stars we can observe this way “pulsars”. The pulses are very regular, and in some cases astronomers can predict when the next ones will arrive to the precision of 10 nanoseconds. Neutron stars have very smooth surfaces, but if they have any “mountains” on them, then they could also continuously emit gravitational waves, which we can detect with LIGO, Virgo and KAGRA. These mountains could be very small and we’d still be able to detect gravitational waves. For example, if the neutron star is spinning more than 100 times per second and 100 parsec away, we could potentially detect a mountain that is less than roughly half a millimeter on the surface of the star!
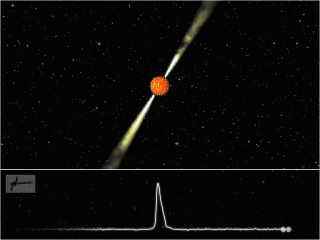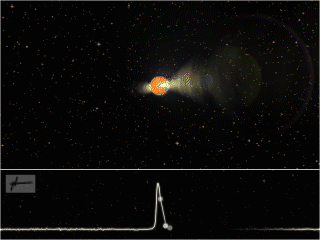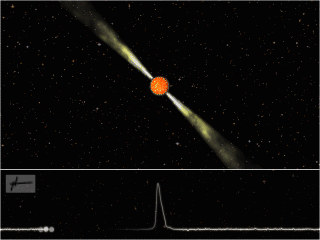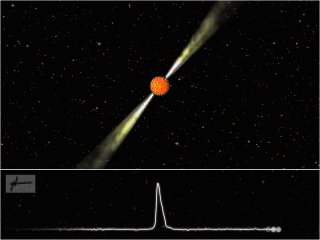
Figure 1: An artist’s impression of a pulsar, showing the rotating neutron star, beams of electromagnetic radiation it emits, and the regular arrival of pulses at a telescope. Image credit: Joeri van Leeuwen, License: CC-BY-AS.
In this study, we use the electromagnetic pulses observed with radio and X-ray telescopes to guide our search for continuous gravitational-wave signals in data from the third observation run (O3) of Advanced LIGO and Advanced Virgo. In a separate study, we have assumed that the frequency of the gravitational waves follows exactly the frequency with which we see electromagnetic pulses arrive. Here, though, we allow for that frequency, and how it changes with time (known as the “spin-down”) to differ slightly from what we observe with electromagnetic waves. We do this to allow for the possibility that the gravitational waves are emitted from asymmetries that exist inside the star, as opposed to on the surface, which is where the electromagnetic waves are emitted. We call this the “narrow-band” approach, and we use it to search for continuous gravitational waves from 18 pulsars. See Figure 2 for our results on the amplitude of gravitational waves we could detect from different pulsars with their respective frequencies.
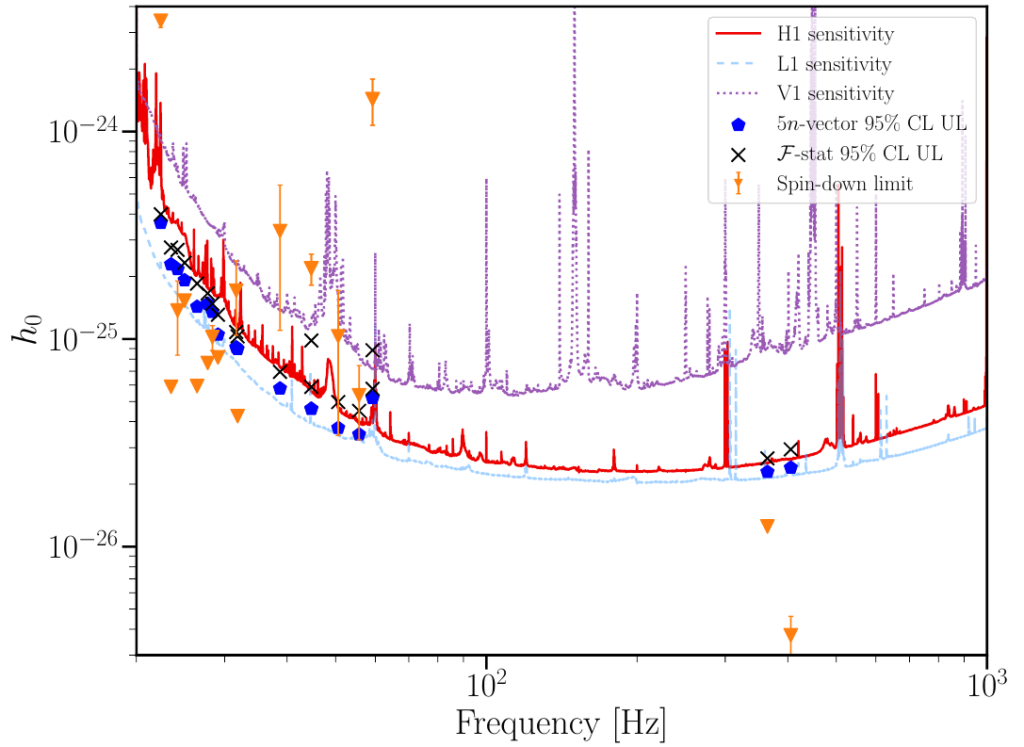
Figure 2 (figure 1 in the publication; click for a larger version): The results of our searches for continuous gravitational waves. The vertical axis is the gravitational-wave strain amplitude while the horizontal axis is the frequency at which the gravitational waves oscillate. The solid lines indicate a pre-search estimate of the level of gravitational waves we thought we could detect with the LIGO Hanford (red), LIGO Livingston (blue) and Virgo (purple) detectors. The orange triangles indicate the spin-down limits for each pulsar. The black crosses indicate the upper limits set using one method to search for continuous waves (“F-stat”), while blue pentagons indicate those set using another method (“5-vec”). For both methods, we get these upper limits by simulating gravitational wave signals from each pulsar and checking how strong they have to be to be detected 95% of the time. We see that in 7 cases, the crosses and pentagons are below the orange triangles, indicating that we set upper limits better than the spin-down limit.
As we said above, most of the time neutron stars rotate very predictably. However, some pulsars undergo “glitches”, which are sudden events where the star rotates faster than before, and so the pulses start arriving more frequently. See Figure 3 for an example of a glitch observed by a radio telescope. This indicates something drastic has happened in the neutron star, but it is still mostly a mystery what exactly goes on inside a glitching pulsar. Stronger gravitational waves could be emitted around or after the time of the glitch, and measuring these could give us unique insights deep inside the neutron star. To test this idea, we also search for gravitational waves after pulsar glitches that were observed in radio or X-ray during O3. We search for shorter-lived gravitational-wave signals that last between 1 hour and 120 days after 9 different pulsar glitches.
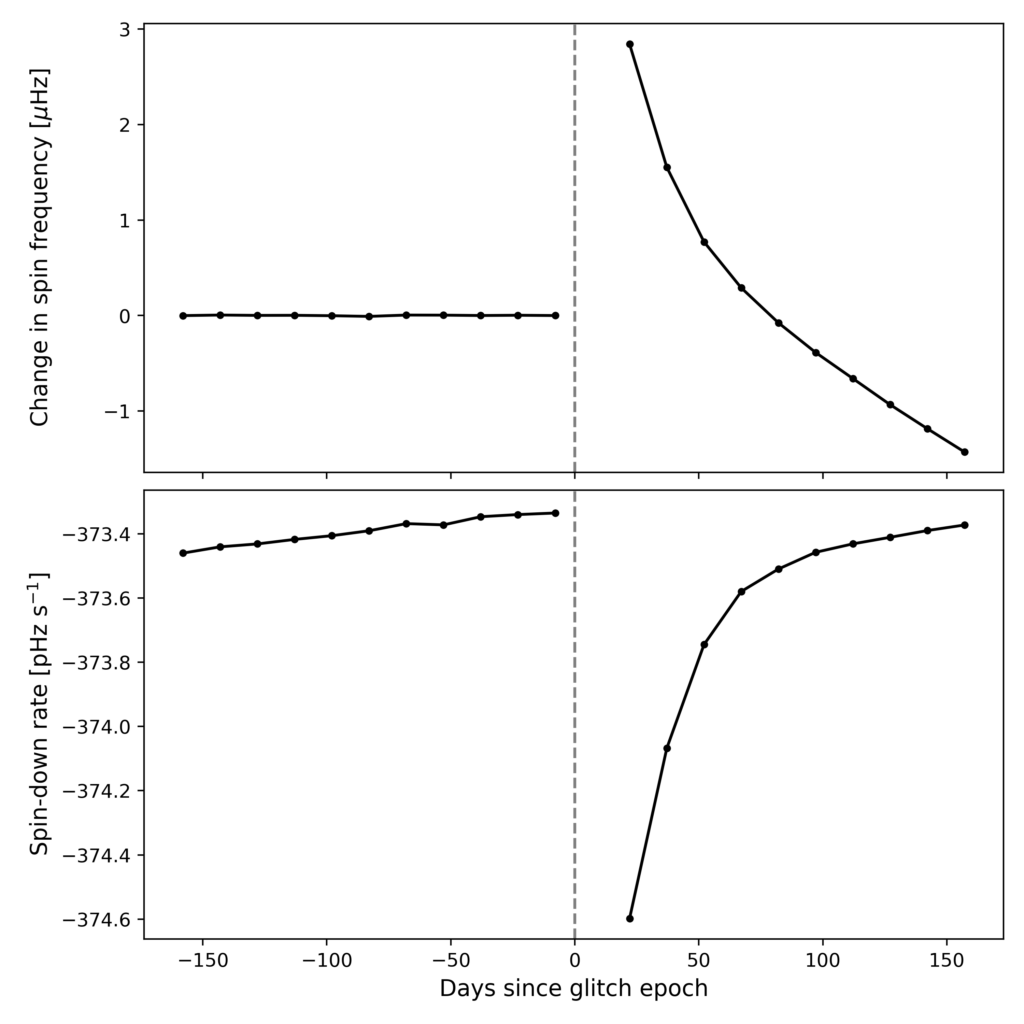
Figure 3: A glitch observed in the Crab pulsar in 2004, using the radio telescope at Jodrell Bank Observatory. In the top panel, we can see how the observed spin frequency of the pulsar is quite constant for many months, but then between two observations it jumped up by several μHz (millionths of a Hertz). (For comparison, the Crab’s actual spin frequency is about 30 Hz.) The spin frequency then decreases again over the following months. Similarly, in the lower panel, the spin-down rate (the change in spin frequency, measured in pHz per second, where a pHz is one millionth of a millionth of a Hz) was steadily but slowly increasing before the glitch, but then jumped downwards before recovering to a steady trend again. (Credit: Pulsar and Time Domain Astronomy Group, University of Manchester)
In the end, we have not found convincing evidence for gravitational waves from any of the neutron stars in these searches. So we use our results to set upper limits on how strong the gravitational-wave emission could possibly be based on how sensitive our detectors are, how much data we have, and where the neutron stars are located. We have shown these limits in Figure 2 with black crosses and blue pentagons. For comparison, we can also set another type of limit on the gravitational-wave emission strength by a simple physical argument: the spin-down observed by radio and X-ray telescopes means the pulsar is losing energy over time, which must correspond to energy lost by the pulsar through the emission of electromagnetic or gravitational radiation. If we assume all of that energy is being emitted in gravitational waves, then we can say how strong the signal could at the very most be. These spin-down limits are shown with orange triangles in Figure 2. In 7 of the 18 pulsars we searched for continuous emission, our observational upper limits set from the gravitational-wave search were below these spin-down limits set by energy arguments. This means that we know at least some of the energy released by these pulsars must be in something other than gravitational waves.
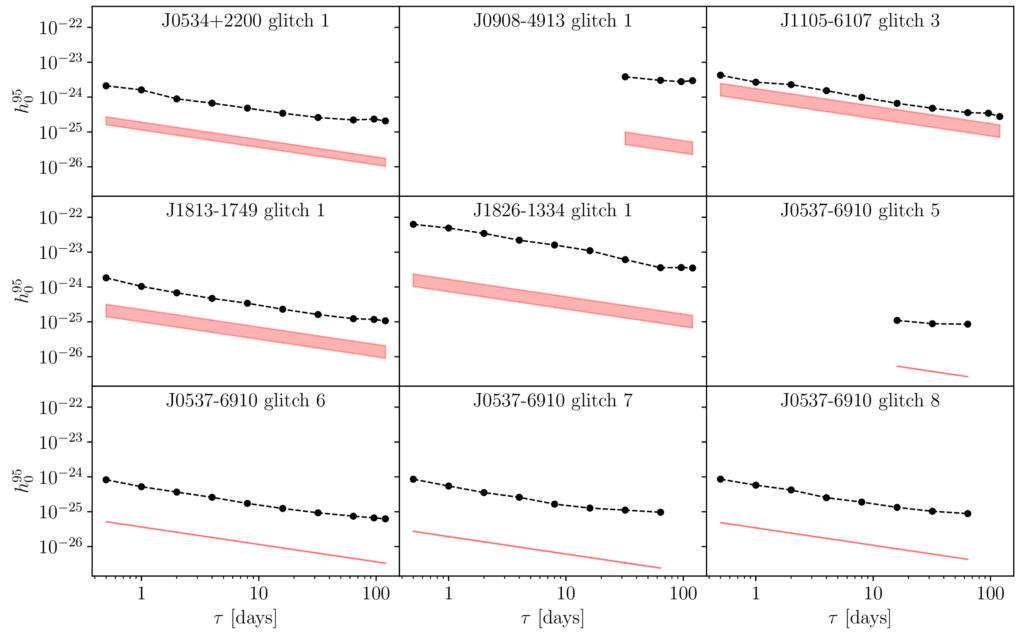
Figure 4 (figure 7 in the publication; click for a larger version): The upper limits on gravitational-wave strain amplitude we obtained by looking at the data around and after pulsar glitches which were observed with electromagnetic telescopes in the timing of 6 pulsars during O3. Each panel shows the upper limits for one search, where 5 pulsars had a single glitch and hence a single set of results each during O3, while the “Big Glitcher” J0537–6910 had four glitches in O3 and is present with four sets of results. The upper limits h095 are obtained similarly as for Figure 2, that is as the strain value at which 95% of simulated signals are successfully recovered with our search method. However, here we have searched for transient signals, where shorter signals are more difficult to detect. So these upper limits (black curve and data points) are shown as functions of signal duration 𝜏 (in days), and are generally lower (more constraining) towards longer durations. For comparison, the red band in each panel shows an indirect estimate of how strong a signal from that pulsar glitch could realistically be, taking into account the energy released in the glitch based on the distance to the pulsar, its rotation frequency, and how much that frequency increased in the glitch. As our observational results do not reach below this indirect estimate for any of the glitches, unfortunately we are not yet sensitive enough to actually probe the physics of what may be going on inside a neutron star during a glitch. (One might wonder why some of the curves are not covering the whole range of 𝜏 values. This is because we do not have gravitational-wave detector data available for the corresponding date ranges after those glitches.)
We can also translate our results into limits on the “size” of a mountain on the pulsar, since the larger the mountain, the stronger the gravitational waves we expect from it. The most constraining limits, for PSR J0711–6830, set the maximum mountain size to be 0.17 mm (assuming a 10 km radius star). Proportionally, if the Earth were otherwise a perfect sphere, then the “mountain” we’re talking about here would be about the size of a soccer ball! In the case of the post-glitch search, the limits due to energy arguments were lower than the limits set by the search for all of the glitches we observed, meaning we still need to wait for future improvements to our detectors to set physically meaningful constraints from that type of search.
While we did not find gravitational waves in this search, rotating neutron stars remain a promising potential source. We look forward to performing the search again with the more sensitive data that will come with LIGO, Virgo and KAGRA’s 4th observing run, which is currently expected to start in late 2022.
Find out more
- Visit our websites:
- Read a free preprint of the full scientific article here or on arXiv.org

