Neutron stars (NSs) are the outcome of a supernova explosion, the remnant of a former star with a mass between 10 and 25 times the mass of the Sun. These compact objects have a typical radius of 10km and a mass similar to that of our Sun, making NSs one of the most extreme environments in which matter has ever been observed. Nowadays, the structure and composition of these compact objects is an active and interdisciplinary field of research, joining efforts from the particle physics and the astrophysics communities.
The extreme compactness (or density) of these objects makes them an interesting laboratory to test relativistic effects such as the emission of gravitational radiation. Indeed, the Advanced LIGO and Advanced Virgo detectors successfully detected several gravitational wave events related to the coalescence of two NSs. One of those detections, GW170817, was even accompanied by an electromagnetic counterpart, producing the first ever multi-messenger detection of an astrophysical event via gravitational waves and light.
Continuous gravitational waves (CWs) are another channel through which the inner structure of rapidly-spinning NSs could be probed. NSs are theorized to be able to sustain deviations with respect to a symmetric shape, either because of an imperfection in the outer crust, an oscillating perturbation in the inner structure, or free precession due to misalignments between the symmetry and the rotation axes. As the NS spins rapidly, such deformations would produce gravitational radiation in the form of CWs. This form of gravitational radiation is several orders of magnitude weaker than the ones produced during the coalescence of compact objects; however, they last for long periods of time (months to years), allowing for the integration of long data streams to accumulate a large signal-to-noise ratio.
Searches for this type of signal are divided according to what is known about potential sources. For example, targeted searches focus on NSs for which the sky position and the rotational frequency is known by electromagnetic means, while directed searches point at certain sky locations where an unknown NS could be located. We present the results of an all-sky search, which means we look for CW signals coming from completely unknown NSs coming from any direction in the sky. In particular, we focus on unknown NSs in binary systems.
The expected signal from isolated NSs is a long-lasting wave, the frequency of which slowly diminishes due to the emission of energy through different means such as electromagnetic or gravitational radiation. This spindown effect is slow enough to be neglected, given the population of NSs considered by this search. From the point of view of a detector on the Earth, the signal presents a frequency modulation due to the daily rotation and orbital motions of our planet. This signal is further complicated for NSs in a binary system, as then a second Doppler modulation has to be taken into account due to the relative motion of the source around its companion body.
In this search, we apply a variation of the Hough transform, called BinarySkyHough, which operates using a spectrogram of the data. This spectrogram provides information about which frequencies are the most prominent in the data as the observing run progresses. The basic idea is that a CW signal would show up as a power excess in the spectrogram modulating in a very particular way, as exemplified in Figure 1. We can describe these power tracks using a set of parameters related to the physical properties of the source under consideration, such as its rotational frequency or its sky position; hence, looking for a CW is a matter of identifying significant power tracks in the data.
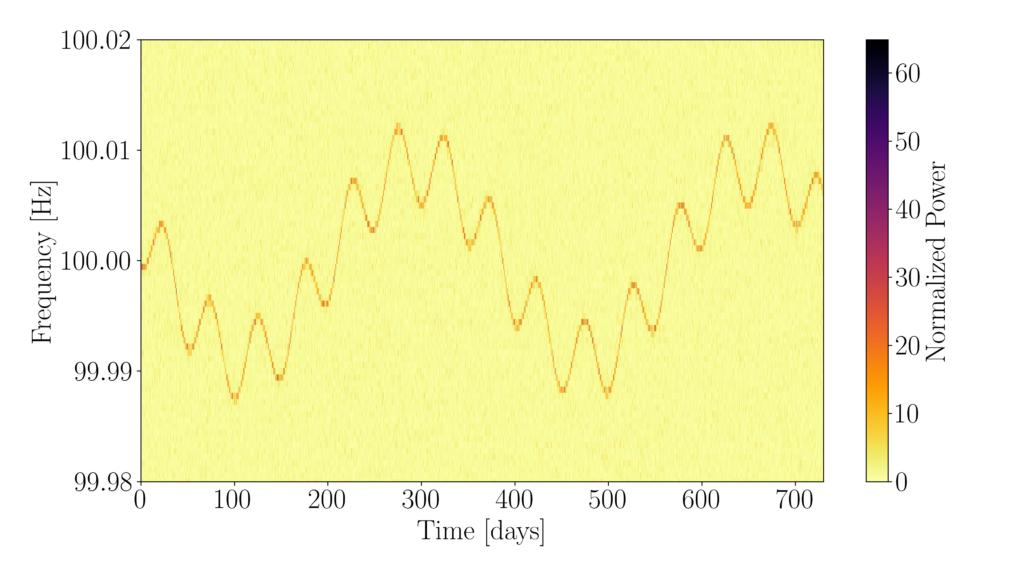
Figure 1: Example of a strong simulated CW as seen in a spectrogram. This signal corresponds to a deformed NS spinning 50 times per second orbiting a companion with an orbital period of 50 days. The overall frequency scale, 100 Hz, is given by twice the rotational frequency of the body. The widest oscillations, with periodicity of 365 days, correspond to the Doppler modulation induced by the orbital motion of the Earth around the sun. The narrower ones, with a periodicity of 50 days, correspond to the orbital motion of the CW source around its companion. The duration of the data stream (2 years) is taken to be longer than the one used in this search (6 months) for illustration purposes.
Due to the inclusion of binary orbital parameters, which describe the shape of a binary orbit, we have to search over more parameters than when we look for single NSs. This poses a problem for typical search algorithms, as the computational cost easily becomes unbearable. In this case the problem can be split into a multitude of similar, smaller tasks, and the search can be sped up with Graphics Processing Units (GPUs) which solve a large number of these subtasks in parallel.
We use data from the early third observing run of the Advanced LIGO and Advanced Virgo detectors, spanning six months of data from April to September, 2019, to search for CWs from unknown NSs in unknown binary systems in the most sensitive band of the detectors. We find no evidence for CW signals. As a result, we estimate the sensitivity of our search by studying the recovery of a population of simulated signals. This sensitivity is initially expressed in terms of the weakest GW amplitude detectable by our pipeline. We obtain the best sensitivity to date for the analyzed parameter space, with the weakest detectable amplitude 60% lower than previous estimations.
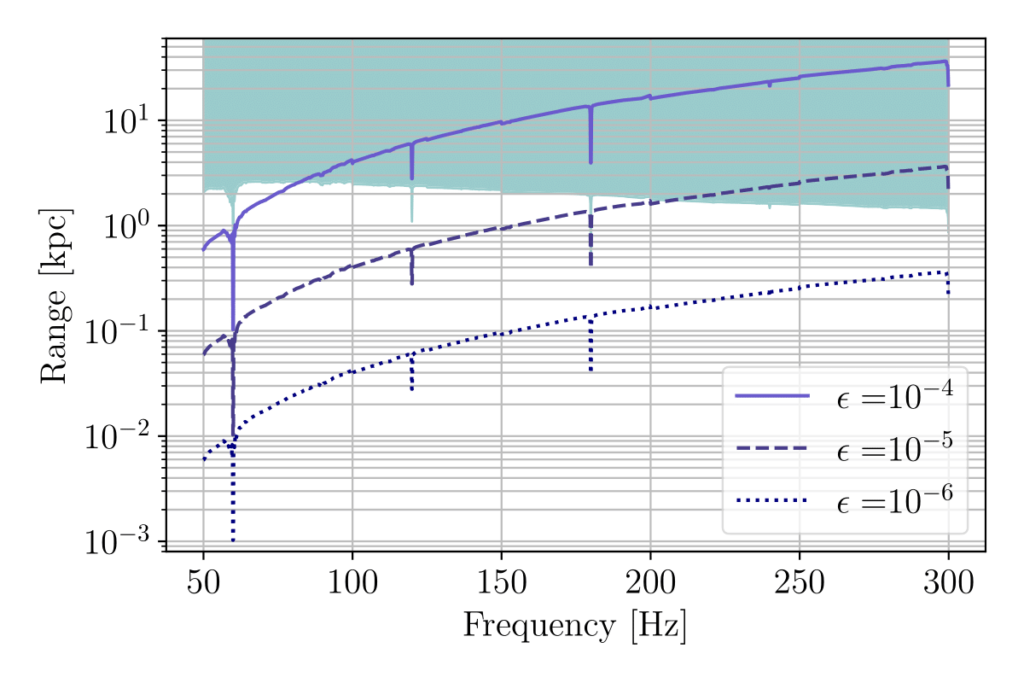
Figure 2: Maximum astrophysical reach covered by our search as a function of frequency. Curves represent different values of deformation, characterized as the ellipticity of a NS. Bigger deformations and higher frequencies tend to produce stronger CWs, allowing us to probe them at further distances. The shaded region implies spindown rates beyond the ones probed by the search, if no other balancing mechanism is assumed. As a reference, the closest known NS to us is located 0.1 kpc away.
We interpret these results in terms of answering two astrophysically interesting questions, namely how far away from the Earth our search was able to probe, and what is the maximum deformation allowed for a CW source within the range probed by our search. Figures 2 and 3 summarize the maximum reach of our search and the maximum deformation allowed for a CW source as a function of the gravitational wave frequency. As previously commented, we consider CW sources with negligible spindown. This assumption sets an implicit limit in the maximum deformation being probed for a NS, represented by shaded regions in said figures. In other words, if no balancing mechanisms are in place, shaded regions are excluded from our results since they would imply higher spindown rates than the ones covered by this search. A possible balancing mechanism countering the NS’s spindown could be the accretion of matter from the companion body. These results show the increasing improvement of the Advanced LIGO and Advanced Virgo detectors as they reach their design sensitivity, allowing us to approach upper bounds on NS properties closer and closer to theoretical expectations.

Figure 3: Maximum deformation allowed for a NS within our search’s reach as a function of frequency. These curves represent how deformed a NS should be to produce a CW detectable by our search. Since CW amplitude decays with distance, closer sources are constrained to have lower ellipticities than those farther away. The shaded region implies spindown rates beyond the ones probed by the search, if no other balancing mechanism is assumed.
Find out more:
- Visit our websites: ligo.org, www.virgo-gw.eu
- Read a free preprint of the full scientific article here.
- Read an introduction to continuous gravitational waves here.

