Imagine a magnifying glass as big as a galaxy and what it will do to light or gravitational waves traveling through the cosmos. Through the phenomenon of “gravitational lensing”, massive astrophysical objects can act as such giant lenses. In this study, we have looked for lensing signatures in the gravitational-wave signals detected in the first half of the third LIGO-Virgo observing run, called O3a for short.
Gravitational lensing – Einstein’s prediction and its rich applications in astronomy
The theory of general relativity postulates that massive astronomical objects curve space and time near them, bending the paths of light. In other words, they act as gravitational lenses. Such lensing can magnify distant objects, split them into multiple images, or deform them into long arcs or “Einstein rings” (see figure 1). Observations of gravitational lensing are widespread in astronomy across the electromagnetic spectrum. Historically, lensing has provided us with the first test of Einstein’s theory during the 1919 solar eclipse. More recently, observations of weak lensing have been used to map the distribution of mass in the universe, making a compelling case for dark matter. Lensing also allows astronomers to study exoplanets that cause periodic variations in their star’s brightness as they move in front of it. Additionally, lensing enables us to uncover massive objects and structures in the cosmos that would otherwise be too faint to detect. To be sure, gravitational lensing has become a standard tool in astronomy, astrophysics, and cosmology.
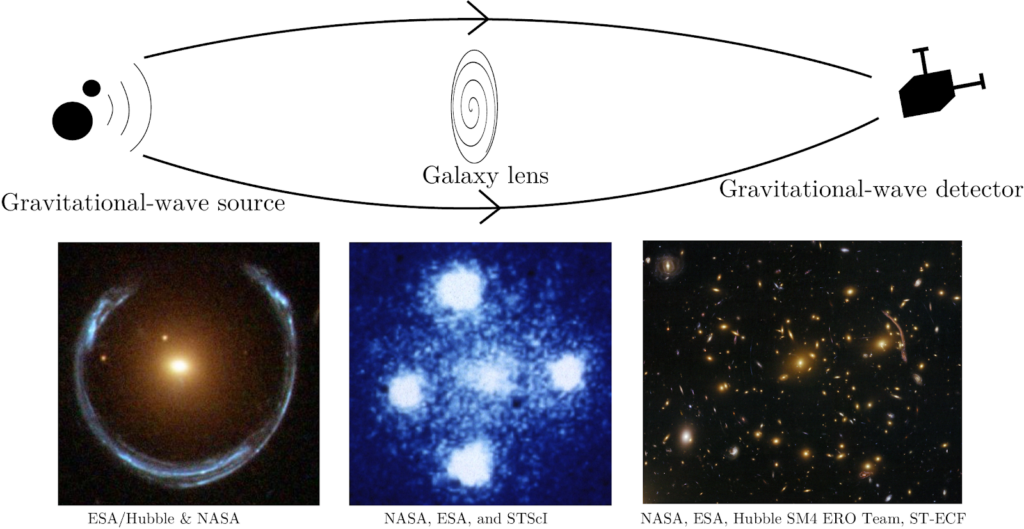
Figure 1: When light travels near massive astrophysical objects, its path is curved due to gravity, resulting in gravitational lensing. Such a phenomenon can produce Einstein rings and crosses, statistical distortions in the background light from galaxies, and many other intriguing observations. Similarly to light, gravitational waves can be lensed. However, the methods to detect and make use of gravitational-wave lensing are entirely different. Instead of image shape distortions or transient brightening of stars, we focus on repeated gravitational-wave events and frequency-dependent distortions in the gravitational waveforms.
What can gravitational lensing do to gravitational waves?
Like electromagnetic waves, gravitational waves can be gravitationally lensed by intervening objects, such as stars, black holes, galaxies, and galaxy clusters. (See figure 1). However, while the theory behind the lensing of gravitational waves is similar to that of light lensing, the methods to detect it are entirely different due to fundamentally different sources and detectors. In particular, we may detect lensing magnification as an overall amplification of the waves. This magnification would cause binary merger signals to appear as coming from closer and higher-mass sources than they really do. Multiple images would appear as “repeated” events: near-identical events appearing minutes to months (or sometimes years) apart. As the lens will typically produce image separations that are far too tiny to be resolved with the current detectors, the events appear to come from the same sky location. On the other hand, microlensing produces tiny lensing time delays, which can cause multiple lensed waveforms to overlap at the detectors and produce waveform “beating patterns.”
What can we learn from detecting lensed gravitational waves?
Once identified, lensed gravitational waves could give rise to several exciting scientific pursuits. When the lens system is sufficiently unique, one could locate merging black holes, invisible to conventional telescopes, by combining gravitational-wave and electromagnetic lensing surveys. When an electromagnetic counterpart accompanies the lensed waves, precision cosmology studies may become feasible owing to the sub-millisecond lensing time-delay gravitational-wave measurements. By contrasting the time delays between lensed gravitational waves with their transient electromagnetic counterparts, one could measure the speed of gravity relative to light. As lensed gravitational waves allow us to observe the same event multiple times at different detector orientations, they can also probe the full polarization of the waves, testing general relativity and alternative theories. Microlensing, on the other hand, might help in studying populations of objects such as primordial and intermediate-mass black holes. Once observed, lensed gravitational-wave observations will allow for new scientific studies of fundamental physics, astrophysics, and cosmology.

Figure 2: This diagram demonstrates how the presence or absence of detectable lensed gravitational waves improves our knowledge of the compact binary merger rate (vertical axis) throughout cosmic history, with the horizontal axis giving the cosmic redshift z. (The present day is at z=0.) We already have some overall idea about the merger rate, as indicated by the blue region in the diagram, from our catalog of observations, which you can read more about in this summary. Knowing whether or not there are detectable lensing effects in the data constrains the high-redshift (early universe) merger rate, as indicated by the red region in the diagram. This is because lensing can magnify signals so that we are able to detect them from further away. In this graphic, the quantity shown on the vertical axis is technically the merger rate density, that is, the number of merging events per year in a unit volume of one cubic Gigaparsec (Gpc). The different lines represent results for different lensing situations: galaxy-scale lenses (G) and cluster-scale lenses (C) as well as situations where only a single (S) or both (D) images produced by a double-image lensing event are detected as gravitational-wave events.
What we looked for in O3a data, and what we found
In the current study, we have searched for lensing signatures in the gravitational-wave signals from compact binaries detected by Advanced LIGO and Advanced Virgo during the O3a observing run. We have forecast how frequently lensing occurs at current detector sensitivity and determined how even the absence of detectable strong lensing effects already constrains the compact binary merger rate in the distant universe (see Figure 2). We also demonstrated how the absence of an observable stochastic gravitational-wave background improves our knowledge of the rate of lensing. Furthermore, we have studied the idea that lensing magnification could help to explain the exceptionally high masses we see in some of our detected events (like GW190425 or GW190521). We have also searched for multiple lensed images in the detector data, comparing how likely any given pair of signals are to either be lensed copies from the same source or to be produced by unrelated sources. We have found several candidate pairs that resemble each other closely (see Figure 3), just as lensed images of a single source would, but in the end have found no support for these to be actually lensed, after we have considered more realistic assumptions on the population of source systems, the selection effects of our searches, and the expected rate of lensing at the current sensitivity. Finally, we have searched for the characteristic “beating pattern” effect of microlensing on the waveforms of detected events, finding no evidence for these in the 36 tested events (see Figure 4). In summary, our comprehensive study for gravitational-wave magnification, multiple-image, and microlensing signatures on O3a data has uncovered no compelling evidence for gravitational lensing.

Figure 3: The most promising pairs of potentially lensed events from O3a (those included in the second gravitational-wave transient catalog GWTC-2), in the sense of high overlap between their estimated properties, including e.g. the masses and spins of the merging objects. The degree of overlap is ranked on the vertical axis. The horizontal axis tells us if the time delay between the pairs is more consistent with lensing (assuming a galaxy acts as the lens, leading to short expected time delays and be ranked higher) or with two unrelated events (which would on average produce longer time delays and be ranked lower). The dashed lines tell us that, combining both measures, none of the pairs show significant evidence for lensing (measured in the conventional “sigma” levels). Still, to dig deeper, we also performed more detailed follow-up analyses and also included population models and selection effects; in the end, all candidate pairs seem consistent with independent mergers that just happen to have similar properties, without lensing being involved.
Future outlook
In the future, it will be possible to dig deeper into lensing effects on gravitational waves with more sensitive analysis methods and more detailed lens modeling. Electromagnetic follow-up observations of lensing candidates, even if they are not significant enough based on the gravitational-wave data alone, could also be promising for identifying the possible host galaxies and lenses. Further upgrades to the current generation of detectors and extension of the global network will continue to improve the chances of detecting clear lensing signatures. Once third-generation and space-based detectors (e.g. the Einstein Telescope, Cosmic Explorer and LISA) come online in the 2030s, many other exciting possibilities will become feasible.
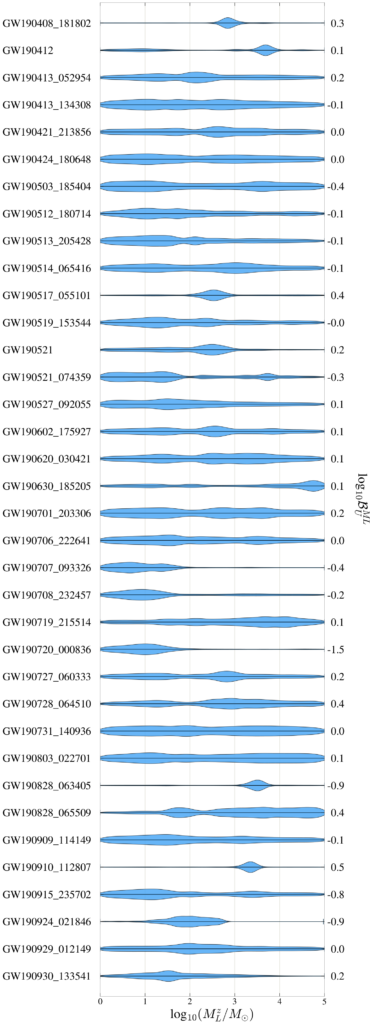
Figure 4: Some of the results from testing 36 events from O3a for frequency-dependent microlensing “beating patterns”. Click the image for a full version. The contours show how likely certain values of the lens mass are given the measured data, assuming the event has experienced microlensing. However, we found no actual evidence for this to be the case for any of these events. The values listed at the right of the figure are Bayes factors, a statistic telling us whether lensing or no lensing is the more likely explanation for the measured data. Since they are all negative or close to zero, this tells us that none of the events require microlensing to explain their frequency evolution.
Find out more:
- Visit our websites:
- Read a free preprint of the full scientific article here or on arXiv.org.
- The final version of this work was published in the Astrophysical Journal and is also freely accessible.
- Watch a Youtube recording of a Zoom webinar presentation about this paper that was held on May 27, 2021.

