Individual gravitational-wave events from the mergers of binary systems consisting of compact objects like black holes and neutron stars can reveal the properties of unique single sources. However, a population of such events is needed to shed light on how these systems form and evolve throughout the Universe. We are particularly interested in measuring the distributions of the mass and spin of compact objects, since these properties allow us to learn about the processes leading to their formation.
Scientists have focused on two ways, or “channels”, through which these binaries could form in nature. In the isolated binary evolution channel, compact binaries evolve together from pairs of massive stars, each of which eventually explodes and leaves behind a remnant neutron star (NS) or black hole (BH). In the dynamical formation channel, neutron stars and black holes couple up in dense environments like globular clusters or nuclear star clusters. Both of these formation channels leave a unique imprint on the observable properties of the compact objects that we detect in gravitational waves. We expect the sources detectable by LIGO and Virgo to broadly cover the mass range between one and one hundred times the mass of the sun (denoted by the symbol M⊙). However, different astrophysical processes may lead to gaps across this mass range where we don’t detect any black holes or neutron stars. For example, previous observations of compact objects both in X-rays and gravitational waves indicated the presence of a lower mass gap in the range of 3 to 5 M⊙ between the most massive neutron stars and the least massive black holes. This could potentially be explained by the physical mechanism governing how massive stars die. An upper mass gap for black holes in the range of about 50 to 120 M⊙ is also predicted due to pulsational pair instability supernovae. In this case, the outer layers of the dying star are ejected, leaving either a lower-mass black hole or no remnant at all. Thus, the presence of either of these gaps would allow us to learn about how massive stars end their lives.
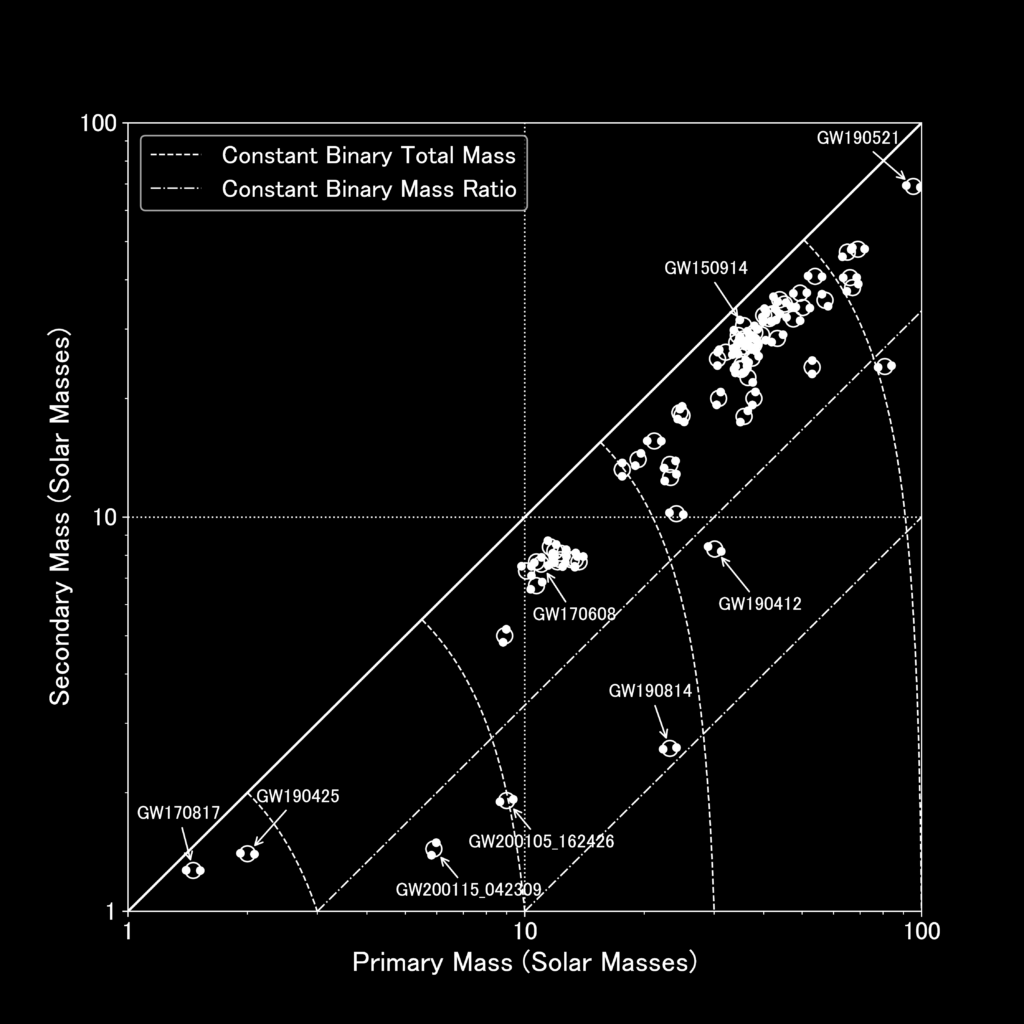
Figure 1: Binaries included in the population analyses performed in our paper, with primary mass on the horizontal axis and secondary mass on the vertical axis. Individual events of interest are marked, along with lines of constant binary mass ratio and total mass. (Credit: LIGO-Virgo-KAGRA Collaboration / IGFAE / Thomas Dent.)
Another important signature of the formation history of a compact binary system is the orientation of the axis of rotation (spin) of its components relative to the axis of the orbit. For example, the tilt of the Earth’s spin axis relative to its axis of rotation about the Sun is what causes the seasons. Compact binaries formed in isolation usually have their spin axes aligned with the axis of the orbit, while those formed dynamically can have their spins pointing in random directions. A third key observable that can be probed with gravitational waves is the distance at which the mergers occur, which can be expressed as a redshift via Hubble’s law. The redshift distribution can tell us about the star formation rate at different points in the Universe’s evolution and the composition of the universe (what elements it’s made of and their relative abundances). This is because the stars’ composition influences how quickly they evolve into compact objects that eventually merge. Thus, measuring the distributions of the masses, spins, and redshifts of compact binary mergers, along with possible correlations between these parameters, is a key target for gravitational-wave astronomy.
Models and Methods
In this work, we use a set of 74 compact binary mergers identified in LIGO–Virgo data up to the end of the third observing run including 70 binary black hole (BBH) events, two binary neutron stars (BNS), and two neutron-star black hole (NSBH) mergers. These events are chosen based on the confidence with which they were detected, to ensure that we are not contaminating our population with noise events that are not astrophysical. In order to constrain the overall population properties of compact objects, we first obtain estimates for the parameters (masses, spins, and redshift) of each individual event and then combine them, taking into account the uncertainty on the individual-event measurements. We then apply several different models for the mass, spin and redshift distributions to the whole population to determine which model offers the best fit to the data. Some of the models are governed by parameters that can be traced back directly to an astrophysical process. One example is the minimum black hole mass, which would tell us something about the presence or absence of the lower mass gap. Other models are more flexible to accommodate unexpected features of the data but not all their parameters are necessarily related to an astrophysical phenomenon.
The compact objects we detect in gravitational waves are not a fair sample of the overall population produced in nature. The strength of the gravitational-wave signal increases with the mass of the system and decreases with the distance (or redshift), so we can observe more massive mergers out to larger distances. We account for this “Malmquist bias” by simulating signals from a population of sources with randomly distributed parameters and then measuring which are easier to detect than others. This allows us to correct for the observational bias.
The overall population of compact objects
When we model all compact object mergers together instead of separately, we estimate the rate at which they occur per unit volume in the universe and per unit time to be between 71 and 2200 mergers per Gigaparsec cubed per year. (1 Gigaparsec = 1 billion parsecs, where a parsec is a unit of distance equal to about 3.25 light years). If we draw the line between neutron stars and black holes at 2.5 M⊙, we obtain the following ranges for the rate of each subpopulation of mergers: (13.0 – 1900.0), (7.4 – 320.0), and (16.0 – 130.0) per Gigaparsec cubed per year for BNS, NSBH, and BBH, respectively. While we detect significantly more BBH sources than the other two classes of signals, they are actually much less common in the Universe. This is because the merger rate of binary systems is a decreasing function of their mass, so that more massive systems produce increasingly rarer mergers. However, a single power-law cannot describe the relation between merger rate and primary mass across the whole binary population from the lightest neutron stars to the heaviest black holes. Our data suggest a dropoff in merger rate above neutron star masses, but it is not clear if there is a distinct gap before the black hole mass range. We will need more data to definitively determine if this feature exists.
Mass distribution of neutron stars
Next, we estimate the mass distribution of neutron stars detected in gravitational waves. Previous measurements of the neutron star mass distribution have used observations of neutron stars in our own galaxy detected as pulsars, which emit in radio or X-rays at regular intervals due to their fast rotation and strong magnetic fields. While the pulsar measurements prefer a mass distribution with two peaks, we find that the neutron stars observed in gravitational waves favor a single-peak distribution that has more support at high masses compared to the galactic distribution. This could indicate that the extragalactic population observed with gravitational waves is distinct from the galactic distribution observable as pulsars. We find that the maximum neutron star mass is in the range of 1.8 to 2.3 M⊙, consistent with pulsar observations.
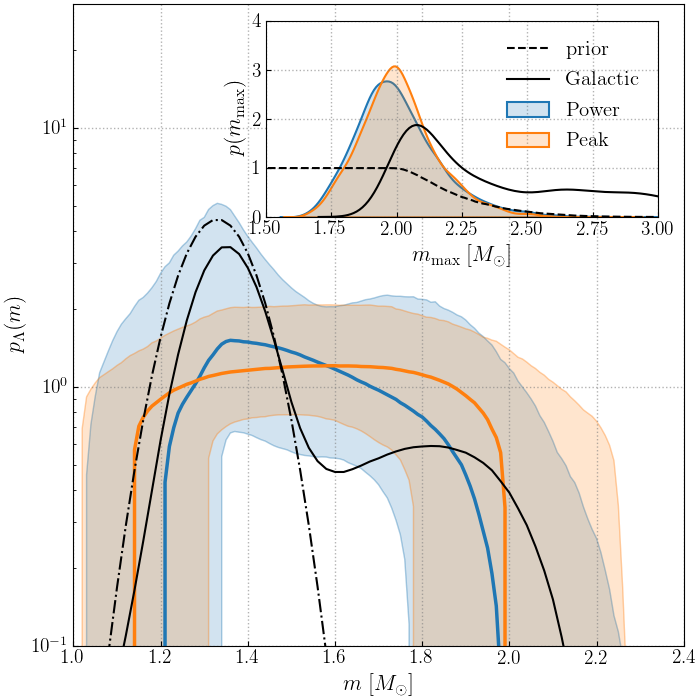
Figure 2 (Fig. 7 of our paper): Mass distribution of neutron stars in compact object binaries observed in gravitational waves. The vertical axis gives the probability of observing a neutron star with mass on the horizontal axis measured in solar masses. The solid blue and orange curves show the inferred distributions under two different model assumptions, while the light shaded areas show the 90% uncertainty on the measurement. The dashed-dotted black line shows the distribution inferred from galactic double neutron star systems, while the solid black line shows the distribution including all galactic neutron stars. The inset shows the probability distribution for the maximum neutron star mass with a similar color scheme. In this case, the vertical axis gives the relative probability that the maximum neutron star mass is the corresponding value on the horizontal axis. The dashed black line shows the initial guess for the maximum mass before the data were analyzed.
Black hole properties
Compared to our previous constraints on the black hole mass distribution, we now prefer more unequal-mass binaries and a higher fraction of low-mass events in the population. Our new, more flexible models identify two new bumps in the distribution of the more massive black hole in each binary (also called the primary) at around 10 and 18 solar masses, in addition to the previously-identified peak at ~35 M⊙. While isolated binary evolution models can explain the clustering of sources in the 8-10 M⊙ range, the origins of the additional peaks are not yet understood. Similarly to the lower mass gap discussed in the full-population section above, we are unable to confidently identify the presence of an upper mass gap for binary black holes. The lack of a sharp cutoff at ~50 M⊙ as predicted from pair-instability supernovae suggests that there may be a component of the population that does not form from isolated binary evolution. Dynamical formation scenarios can lead to hierarchical mergers, where the remnant of a previous merger encounters another compact object companion to merge again. This can result in a mass distribution extending into both the lower and upper mass gaps. Alternatively, the upper mass gap can be filled in by binaries in gaseous environments, since their component black holes can grow in mass via accretion (when surrounding gas falls into the black hole).
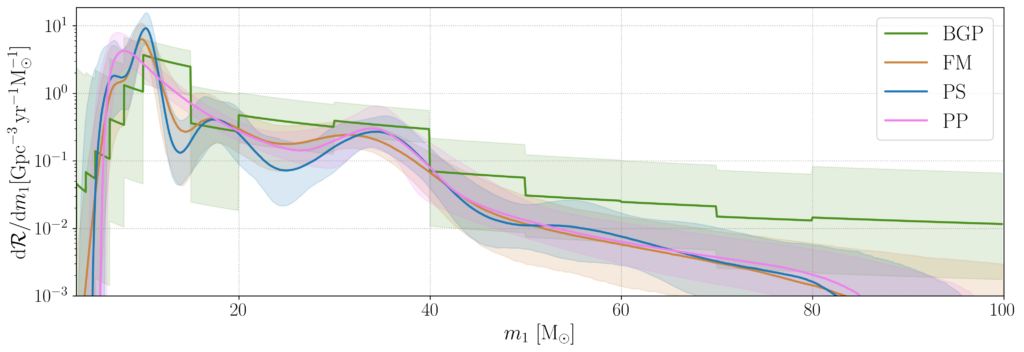
Figure 3 (Fig. 11 of our paper): The primary mass distribution inferred using four different model assumptions shown in the three different colors. Each of the three more flexible models (excluding the pink) recovers evidence for substructure, with significant peaks at ~10 and 35 solar masses and another tentative peak at ~18 M⊙. The vertical axis gives the rate at which systems with the primary mass on the horizontal axis merge in the Universe, and the shaded regions show the uncertainty on each measurement. A higher value on the vertical axis means those masses are more common.
We still think that black holes in binaries have small spins that are not completely aligned with the orbital axis. In fact, the new observations favor a more random distribution of spin tilt angles than before. We now also find a stronger preference for the presence of negative spins in the BBH population, where the spin axis points in the opposite direction entirely from the orbital axis. This is extremely unlikely in the isolated binary evolution scenario, which suggests that at least some of the observed BBHs formed dynamically. We also find that lower-mass systems are more confidently constrained to have small spins, while larger spins are allowed for higher-mass systems. More unequal-mass binaries are found to have larger spins aligned with the orbital axis. Both of these correlations are unexpected theoretically. One potential explanation is that the effect is due to adding together two distinct populations in the mass-spin parameter space, but further investigations will be required to fully explain these effects.
Another new finding from our data is that the merger rate grows with redshift. We know that the star formation rate also evolves with redshift from galaxy observations–meaning that the number of stars available to become compact objects that eventually merge and get detected in gravitational waves changes throughout cosmic time–so we may naturally expect the rate of the eventual mergers to follow a similar distribution. While our previous analyses were consistent with an unevolving (flat) merger rate in redshift, this possibility is now excluded at 99.4% credibility. A precise measurement of the evolution of the merger rate will eventually help us to understand the composition of the universe and the processes by which gas is converted into stars.
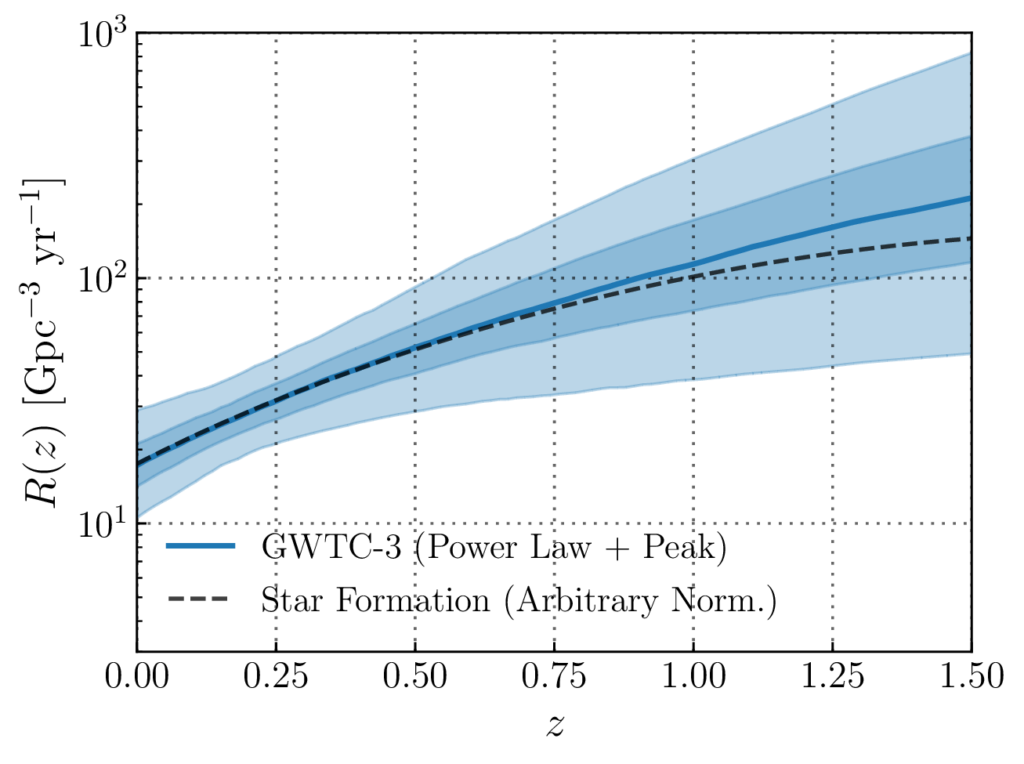
Figure 4 (Fig. 13 from our publication): The median inferred merger rate density on the vertical axis as a function of redshift on the horizontal axis is shown in the solid blue line. The shading shows the 50% (darker) and 90% (lighter) uncertainty regions on the measurement. The evolution of the star formation rate with redshift is also shown in the dashed black line.
Conclusions
Our new, larger catalog of compact binary mergers has allowed us to probe the properties of black holes and neutron stars detected in gravitational waves more precisely than ever before. We are beginning to delve into the formation and evolutionary pathways of the compact objects detectable with LIGO and Virgo. With more data from future observing runs, we expect to eventually confirm the existence of the mass gaps, or lack thereof, and to better understand the unexpected features we have now uncovered. This will help us place new direct constraints on astrophysical phenomena such as how stars die, how compact objects couple up dynamically, and what the universe is made of.
Find out more
- Visit our websites:
- Read a free preprint of the full scientific article here or on arXiv.org

