The mysterious dark matter exists all around us and yet is invisible to us. Such dark matter could be composed of extremely light particles known as bosons, each having a mass of approximately 10-47 kg (that’s a number with 46 zeros after the decimal point, followed by a single “one”). These particles are about 20 orders of magnitude lighter than an electron! If they exist, they could randomly pop into existence near rotating black holes and could scatter, i.e. bounce, off the black holes, extracting energy and momentum from them. Because these bosons have mass, and the black hole exerts a strong gravitational pull, they become bound to it, which allows for successive scatterings and for more energy and momentum to be extracted. There is no limit on the number of bosons that can have a particular energy value, which means it is possible for 1050 of them to exist around the black hole and all extract energy from it!
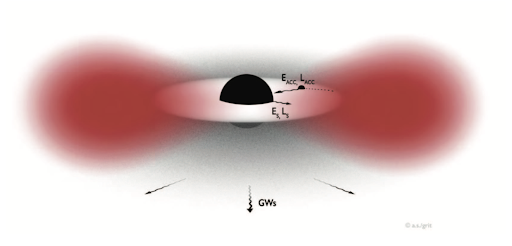
Figure 1: A schematic showing a rotating black hole surrounded by a boson cloud (in red). The macroscopic cloud takes on a dipolar shape because that is the lowest energy state for bosons to fill. Credit: Richard Brito, Vitor Cardoso, Paolo Pani.
The sheer number of particles leads to a macroscopic cloud of bosons forming around the black hole. At this stage, the bosons will annihilate over time, i.e. they will collide with each other, resulting in the emission of gravitational waves at an almost fixed frequency, almost a single tone. Very slowly over time, the cloud will get smaller and smaller as more and more bosons collide with each other, but it could take tens of thousands of years for it to disappear! The time it takes for the cloud to be created is much shorter than the time for the cloud to deplete through annihilation, ensuring that, in our lifetimes, these boson clouds will be emitting gravitational waves.
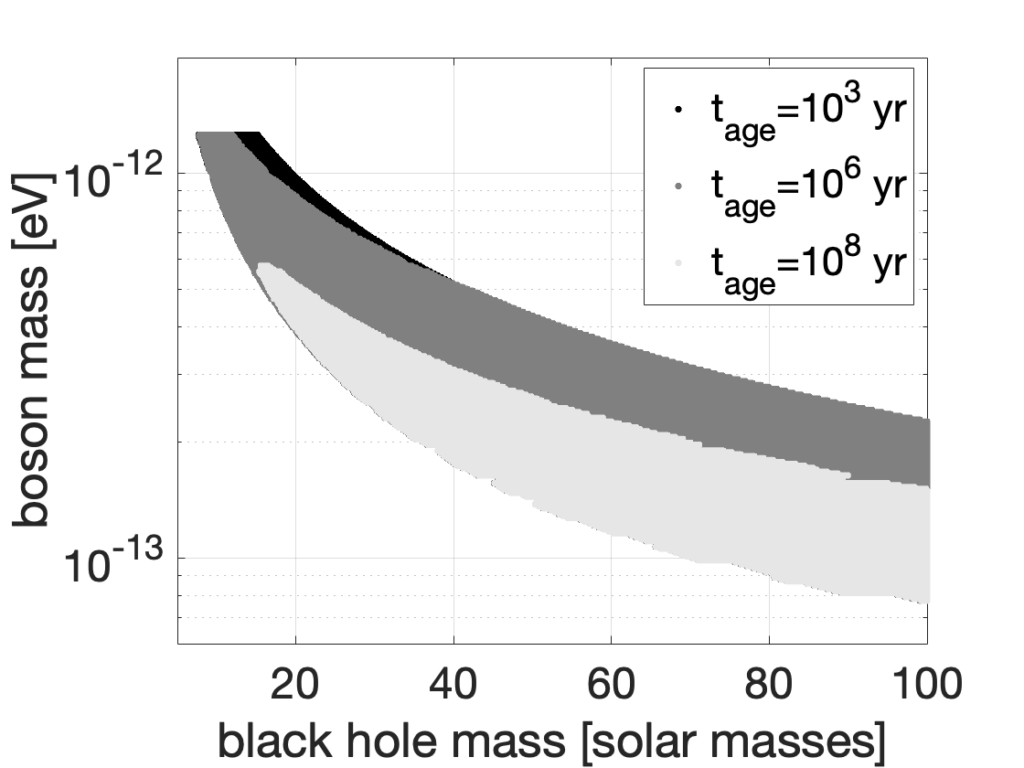
Figure 2 (Fig. 6 in the paper). Here, we assume that black holes with boson clouds could form at a distance of 1 kpc with a spin of 0.9 and could have one of three ages. We exclude the presence of a boson cloud around a black hole over particular mass ranges for the three possible ages given in the figure. Younger black holes emit stronger gravitational waves; hence, the solid-black exclusion region given by tage=103 years (one thousand years) also includes the entire space excluded by systems with greater tage, making it the most constraining of the three ages.
Using the most recent LIGO data, the LIGO/Virgo/KAGRA collaborations performed a search for gravitational-wave signals arising from depleting boson clouds that could come from anywhere in the sky. Such a search is very computationally intensive because we need to analyze each sky position separately at all frequencies, since we do not know the mass of each boson particle, nor where in the sky black holes have formed. Our method breaks the one-year dataset into small chunks of at most a few hours, looks for a monochromatic (i.e. with a single frequency) signal in these chunks, and combines them afterwards. Though we expect the signal to be monochromatic, we wish to also be robust towards uncertainties in the theories that govern gravitational-wave emission from depleting boson clouds. Therefore, we consider the possibility that the frequency of the gravitational-wave signal could wander randomly in time. In both cases, we do not find a significant signal at any boson mass or sky position, and so we set some of the most stringent upper limits on the existence of boson clouds around spinning black holes in our galaxy.
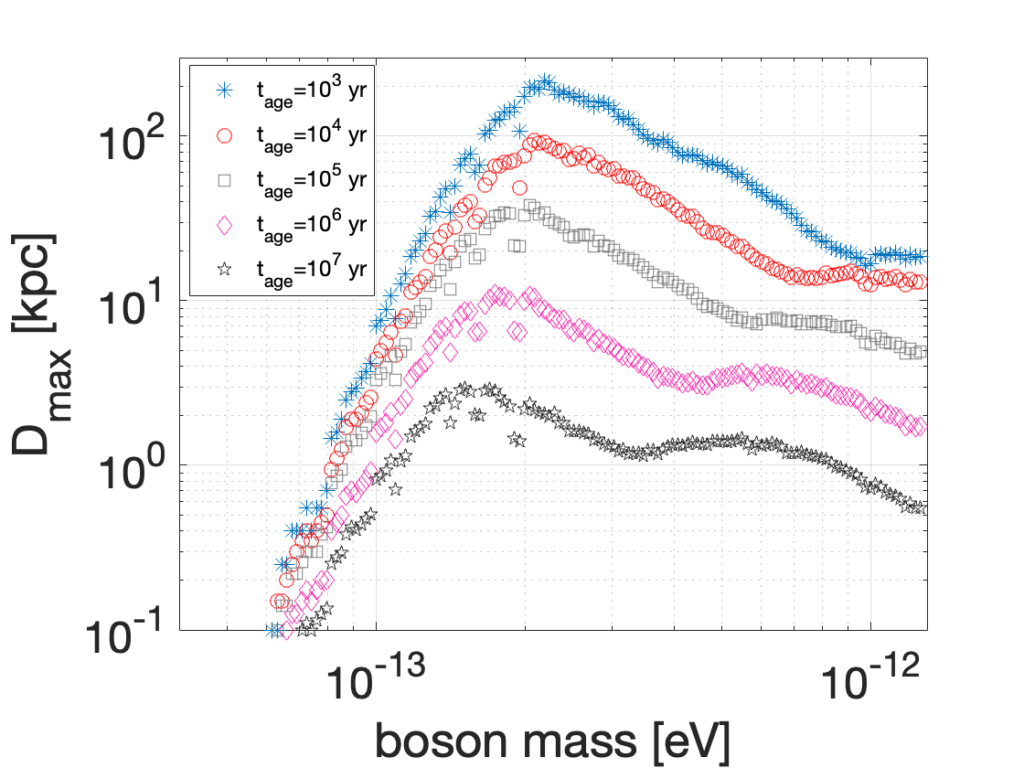
Figure 3: (Fig. 8 in the paper). Maximum distance reached as a function of boson mass, for fixed age of the cloud, for randomly chosen black hole spins and for black hole masses between 5–100 solar masses, chosen according to a particular mass distribution that favors light black hole masses. We can see that the youngest systems with tage=103 years can be constrained at the farthest distance away from us. Furthermore, these results are dependent on the population of black holes that we assumed, and could change if we allow for masses, spins and ages to be distributed in a different way.
We interpret these limits in two ways. First, for a given distance, spin and age of a black hole, we compute the amplitude of the gravitational-wave signal that could have arisen from it for a variety of boson mass/black hole mass pairs. If this amplitude is larger than that derived in the analysis (which doesn’t explicitly assume a depleting boson cloud model), we can exclude the presence of a cloud around a black hole at particular boson masses between 10-13 to 10-12 eV (~10-47 to 10-46 kg) and black hole masses between 5-100 solar masses, respectively. Second, we assume a model for the way that black hole masses are distributed, and for a fixed boson cloud age and random black hole spins, we calculate at what distance a cloud composed of bosons with a certain boson mass would have produced a strong enough signal to be detected. Our results imply that we would have been sensitive to, at best, black hole/boson cloud systems around 100 kpc (over 300,000 light years) away!
Find out more
- Visit our websites:
- Read a free preprint of the full scientific article here or on arXiv.org

