What are gravitational waves?
Since the first detection of gravitational waves in 2015, we have observed a multitude of gravitational wave events. What all these events have in common is that they are transient signals from merging compact objects. These events include the inspiral and merger of pairs of binary black holes, pairs or binary neutron stars and the merger of a neutron star and a black hole. The gravitational wave signals from these events are characterised by an increasing amplitude and frequency over a short time. However, there are still other forms of gravitational waves which we are searching for. For example, signals produced by sources that are continuously emitting gravitational waves with a relatively constant frequency and amplitude.

Figure 1: An artist’s impression of a pulsar/neutron star. Credits: NASA’s Goddard Space Flight Center
What are pulsars (neutron stars)?
A candidate for such continuous gravitational waves are neutron stars, some of which are seen through electromagnetic observations as pulsars. When a star about 8-20 times more massive than the sun uses up its fuel, it will no longer be able to sustain itself and undergoes a massive explosion called a supernova. A neutron star is what remains of the core of the star afterwards. They are incredibly dense, imagine the mass of the Sun (~2×1030 kg) packed into the size of a city (~10 km in radius). We expect these stars to be very rigid, unlike younger stars like our Sun. They also spin at very high rates, sometimes hundreds of times a second (i.e., rotation frequencies greater than 100 Hz) if they have been sped up by the accretion of material from a companion star during their lifetime. This incredible speed corresponds to their surface travelling at ~10% of the speed of light. Their rapid rotation powers intense electromagnetic radiation (from radio through to gamma-rays in some cases) emitted from their magnetic poles in concentrated beams. If the beam is at some point directed at Earth and the rotation axis of the neutron star is misaligned from its poles, we can see the neutron star pulsing like a lighthouse. This led to the name “pulsar”.
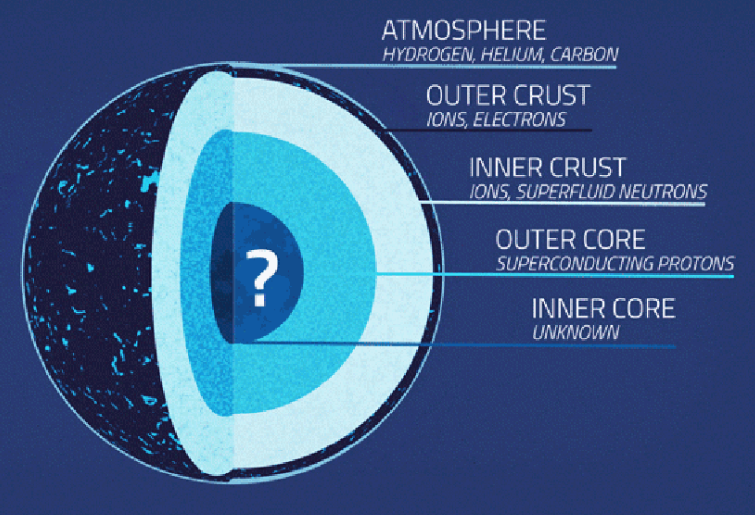
Figure 2 An artist’s impression of a pulsar/neutron star interior. Credits: NASA’s Goddard Space Flight Center
For a pulsar to emit gravitational waves it needs to be rotating with some mass asymmetry about its axis of rotation (mass quadrupole). For example, if a pulsar has some deformation on its crust such as a “mountain”, this would cause it to emit gravitational waves. These mountains might be left over from the conditions during the supernova explosion when the star formed or could be caused during the pulsar’s lifetime such as through accretion. A mountain on a pulsar bears little resemblance to mountains like Everest on Earth. The gravity on the surface of a pulsar is so strong that, according to our measurements, any mountain larger than a few centimeters would be flattened as it crumbled under its own weight. The ellipticity is a way of describing the amount of deformation as a fraction of the radius of the star. Some processes beneath the crust can also cause the emission of gravitational waves, such as through a strong internal magnetic field.
What would the waves look like?
Over their lifetimes, the rotation frequency of pulsars decreases. This is referred to as spin-down. Conservation of energy states that for the rotational energy to decrease, it has to be converted into some other form of energy. If we assume that all the angular energy lost is converted to gravitational wave energy, we can get an upper limit on the wave amplitude on the detectors on Earth. This is called the spin-down limit. When our searches reach sensitivities below this, we can place new upper limits on the amplitude and may even observe gravitational waves themselves. However other mechanisms such magnetic dipole radiation are also likely to contribute to the spin-down, and therefore we expect this upper limit to be an overestimate.
We assume certain relationships between the rotation frequency of the pulsar (as observed through the electromagnetic signal) and the frequency of the gravitational waves that it would emit. In general, we expect the gravitational wave emission to be at twice the rotation frequency of the pulsar. There are also mechanisms which can cause emission at the rotation frequency itself. For example, free precession of the star where its axis of rotation is itself changing, and a superconductive core which is rotating independently of the crust.
Our analysis
This analysis searched for evidence of gravitational waves in the second and third LIGO–Virgo observing runs (referred to as O2 and O3) at both once and twice the rotation frequency of the pulsar. There were 236 pulsars included in the search, including 74 pulsars which weren’t included in the previous analysis of the first and second observing runs. There were 168 pulsars in binary systems and 161 pulsars with frequencies above 100 Hz, called millisecond pulsars. Electromagnetic observations from various observatories provided pulsar position, frequency and frequency measurements which were used to track potential gravitational wave signals in the data through a process called coherent integration.
We have also introduced a new search method designed to detect the dipole radiation present in Brans-Dicke theory. The Brans-Dicke theory, motivated by Mach’s principle, was proposed by Carl Brans and Robert Dicke. The foundations of this theory were built on the previous work of Pascual Jordan as well as Markus Fierz, and sometimes it is also referred to as Jordan–Fierz–Brans Dicke theory. In Einstein’s general relativity, the coupling constant between matter and spacetime is given by G (the Newtonian constant of gravitation). In Brans-Dicke theory, the coupling depends also on a parameter ζ through the relation G(1- ζ). The Brans-Dicke parameter (ζ) is obtained through experiments, and the Cassini experiment in 2003 has imposed the constraint ζ < 0.0000125. Gravitational radiation in general relativity is dominated by a time-varying quadrupole moment, and dipole radiation is prohibited due to the conservation of linear momentum. On the other hand, Brans-Dicke also allows the time-varying dipole moment to generate gravitational waves, as in the case of electromagnetic theory. We can perceive a quadrupole moment as stretching of mass about an axis, whereas a dipole moment gives the distribution of mass away from a point in a particular direction. Moreover, in the case of quadrupole emission, the frequency of the gravitational wave is twice the spin-frequency of the pulsar, whereas in the case of dipole radiation, the waves are emitted at the spin frequency of the star analogous to electromagnetic radiation.
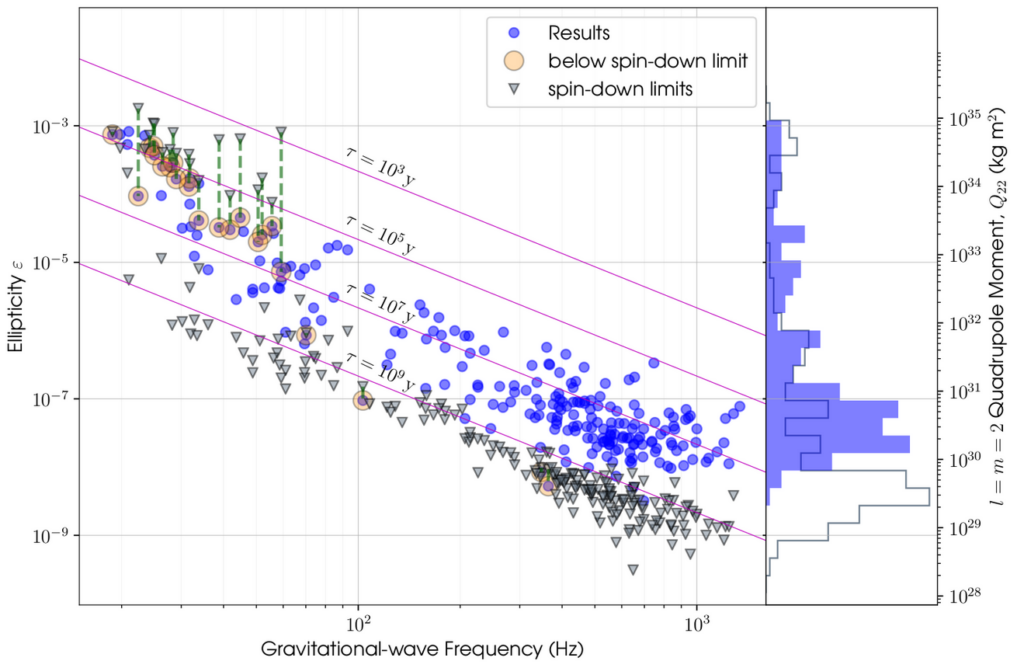
Figure 3: Upper limits on ellipticity and mass quadrupole for all 236 pulsars. The upper limits for each pulsar are represented by blue circles while their spin-down limits are shown as grey triangles. Pulsars for which our direct upper limits have surpassed their spin-down limits are highlighted within a shaded circle with a dotted green line linking the limit to its spin-down limit. Also included are pink contour lines of equal characteristic age assuming that gravitational-wave emission alone is causing spin-down. (Click for a bigger version.)
The results
No evidence was found for gravitational waves from any of the pulsars using the regular search methods or the Brans-Dicke method. However, we have produced updated upper limits on the signal amplitudes and surpassed (produced limits smaller than) the spin-down limits for 23 pulsars, 9 of which did so for the first time. Two millisecond pulsars are included in this number: J0437−4715 and J0711−6830, as well as J0537−6910 which was not analysed in this work but was found to surpass its spin-down limit in a previous analysis. This is exciting because most of the pulsars which surpass their spin-downs are younger pulsars as they are spinning down quicker, therefore providing more energy which can be converted to gravitational waves. Moreover, due to their higher frequencies, lower mountains are sufficient for millisecond pulsars to emit observable gravitational waves. So, for these pulsars our observations provide very stringent limits on the mountain height of fractions of a millimeter. For the Crab pulsar we have improved on the limits calculated in the previous analysis, calculating the upper limit to be the maximum percentage of spin-down being caused by gravitational waves to be less than 0.009% (previously ∼0.02%). This means the majority of the spin-down is caused by other mechanisms. With an ellipticity of 7.2×10-6 this corresponds to a maximum mountain height of ~2 cm (previously ~3 cm). During the fourth observing run — if we are lucky — we may finally observe gravitational waves emitted from pulsars. If not, we shall be able to put more stringent upper bounds on the nearly perfectly smooth shapes of these weird objects.
Find out more
- Visit our websites:
- Read a free preprint of the full scientific article here or on arXiv.org

