The Gravitational Wave Background (GWB) is the superposition of numerous weak and independent gravitational waves generated by different sources, which produces a persistent, incoherent signal across multiple frequency bands, including the LIGO-Virgo-KAGRA (LVK) GW detectors’ frequency range of 10-1000 Hz. GWB sources can be categorized as ‘cosmological’ or ‘astrophysical’ based on their origin. Astrophysical sources include core-collapse supernovae, rotating neutron stars, and the population of unresolved, faint compact binary coalescences (CBCs). The expected background strength for CBCs is now predicted within good approximation, assuming the local observed population of CBCs may be extrapolated to higher redshifts, and the merger rate model is well understood (see Figure 1). Beyond these, there are cosmological sources, such as cosmic strings, inflation, and first-order phase transitions, which can offer insights into the epoch before the emission of the Cosmic Microwave Background (CMB), a period that is otherwise inaccessible through direct observation. Detecting the GWB would represent a major scientific milestone, offering profound insights into both astrophysical and cosmological phenomena. In the nanohertz (i.e. 10-9 Hz) frequency range, multiple pulsar timing arrays – NANOGrav (North America), EPTA (Europe), PPTA (Australia), and InPTA (India) – reported evidence for a stochastic gravitational wave background (SGWB) at a high detection significance for a common-spectrum signal, expected to be produced by a different category of sources than the signal in the LVK frequency range.
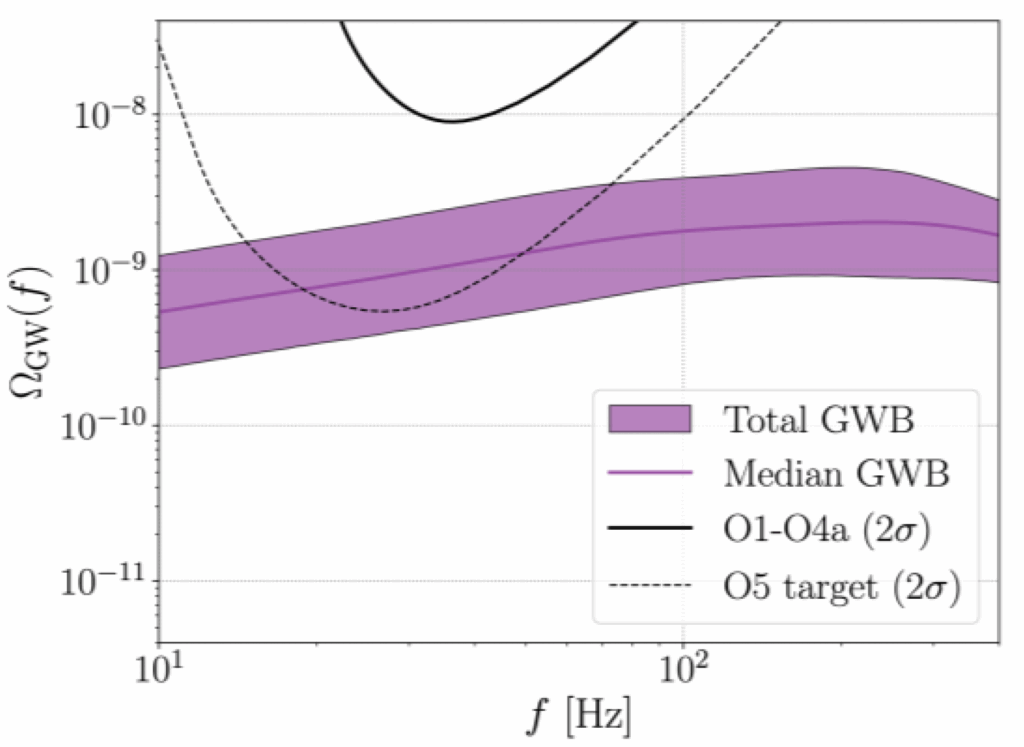
Figure 1: Sensitivity to the GWB as a function of frequency from analysis of the first three observing runs and the first part of the fourth observing run (O1-O4a) is shown by a solid black line, together with the target sensitivity for the fifth observing run O5, shown by a dashed black line. The solid purple line shows the median estimate of the total background (from binary black holes, binary neutron stars and neutron star-black hole pairs) as a function of frequency, while the shaded purple band illustrates 90% credible uncertainties on this background.
Our analysis includes data from Advanced LIGO and Advanced Virgo collected during the first three observing runs (O1–O3), as well as data from the first part of the fourth observing run (O4), during which only Advanced LIGO was operating. We target the frequency dependence of the GWB, modelling the signal as isotropic (i.e. equal in all directions), unpolarized (i.e. with no overall preferred direction of oscillation), stationary (i.e. with statistical properties that don’t change with time) and gaussian (i.e. where those statistical properties can be described solely in terms of a mean and variance) in the limit of long observing time. The signal is also assumed to be weak compared with the detector sensitivity. In this search, data from at least two GW detectors (e.g., LIGO-Hanford and LIGO-Livingston) are cross-correlated to suppress instrumental noise while enhancing sensitivity to a GW signal that is common to each detector. Noise is generally uncorrelated between detectors; however, a stochastic background would induce correlated signals consistent with the light travel time between the detectors and their expected overlap reduction function.
This is the first time we used pygwb, a python-based library that is developed within the LVK collaboration to search for a SGWB. Pygwb offers improved computational efficiency and greater flexibility to customize the analysis. Our analysis technique ensures that – to the best of our knowledge – there is no correlated signal coming from environmental noise, such as instrumental, geological or human-related sources. Furthermore, we mitigated the effect of loud glitches by a technique called gating, which consists of removing each glitch in the time domain. Data from the detectors was cross-correlated and a power law model was used to characterize how the signal varied with frequency. Bayesian inference methods were then used to determine the 95% credible level upper limit on the GWB reference amplitude Ωref either by fixing the value of the power-law spectral index α or averaging (known as “marginalizing”) over this value (see Table 1).
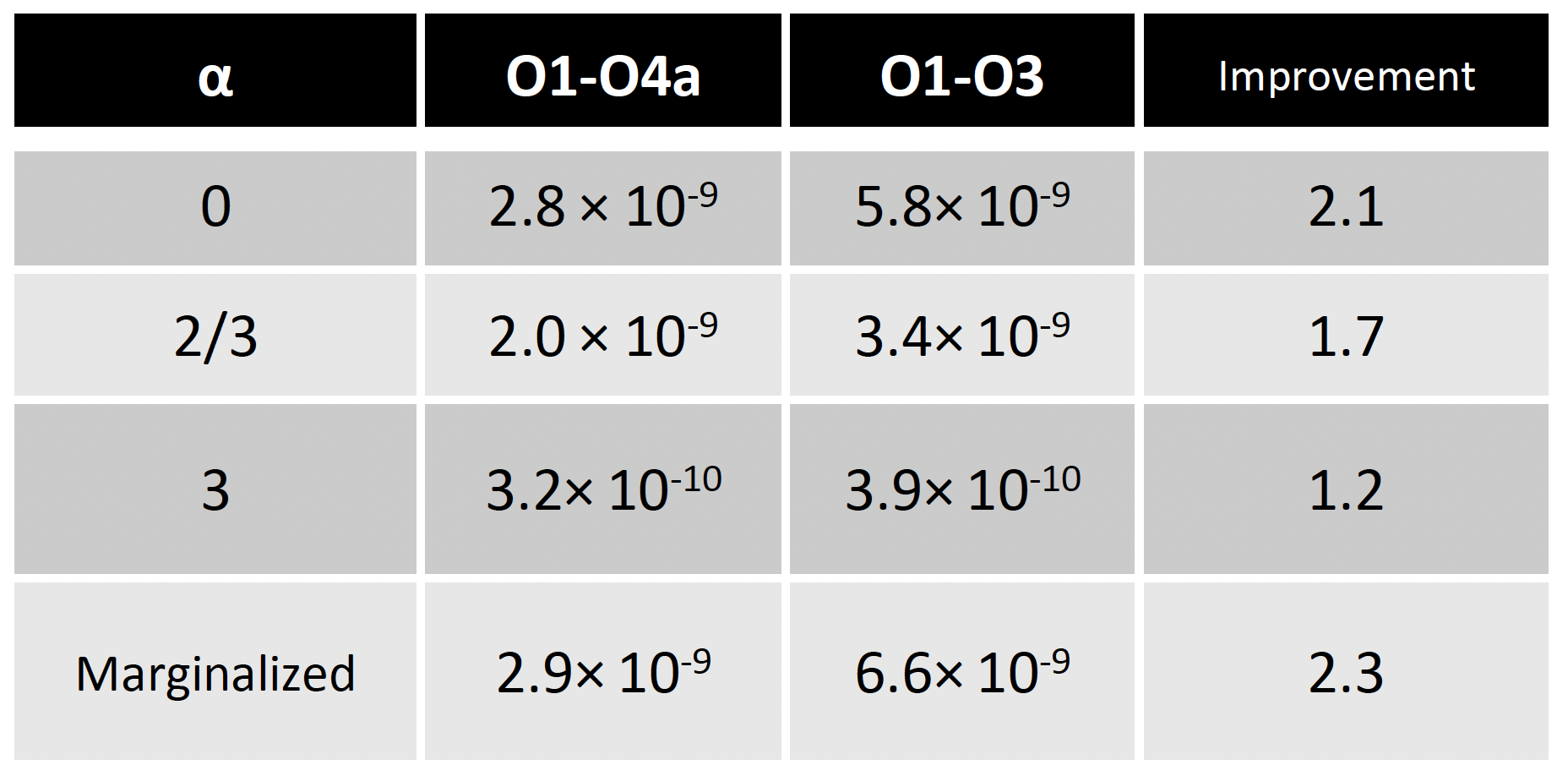
Table 1: Upper limits at 95% credible level on the amplitude Ωref of the GWB assuming a log-uniform prior. The last column shows the improvements with respect to the previous analysis.
We were unable to claim a detection, though we placed more stringent upper limits on the strength of the SGWB than had been published before, due to the inclusion of the latest data from the first part of O4.
We analysed magnetic field data from sensors near each interferometer to investigate globally correlated noise from Schumann resonances. These resonances can mimic gravitational-wave signals by coupling to sensitive components, like end-mirror control magnets, causing false mirror displacements and potentially leading to misidentification of magnetic noise as a stochastic gravitational-wave background. To assess the risk of such contamination, high-fidelity, on-site magnetic field measurements from specialized magnetometers located outside (where the Schumann resonances are expected) and inside the two LIGO observatories are carefully studied, looking for how these measurements are coupled, as well as the coupling of the fields inside the building to the movement of the mirrors.
We performed cross-correlation analyses to estimate magnetic contamination across individual frequency bins. We also examined whether the combined effect of magnetic contamination across multiple frequency bins could exceed our sensitivity threshold. Our conclusion is that our measured estimates of correlated magnetic noise are well below the sensitivity we achieved in the first part of O4, both in individual frequencies and accounting for a sum over multiple frequencies (see Figure 2). Additionally, we implemented a framework, based on Bayesian inference, to simultaneously fit for a GWB and Schumann resonances in our data. Consistent with our other methods, we find no evidence for a signal from either the GWB or Schumann resonances.
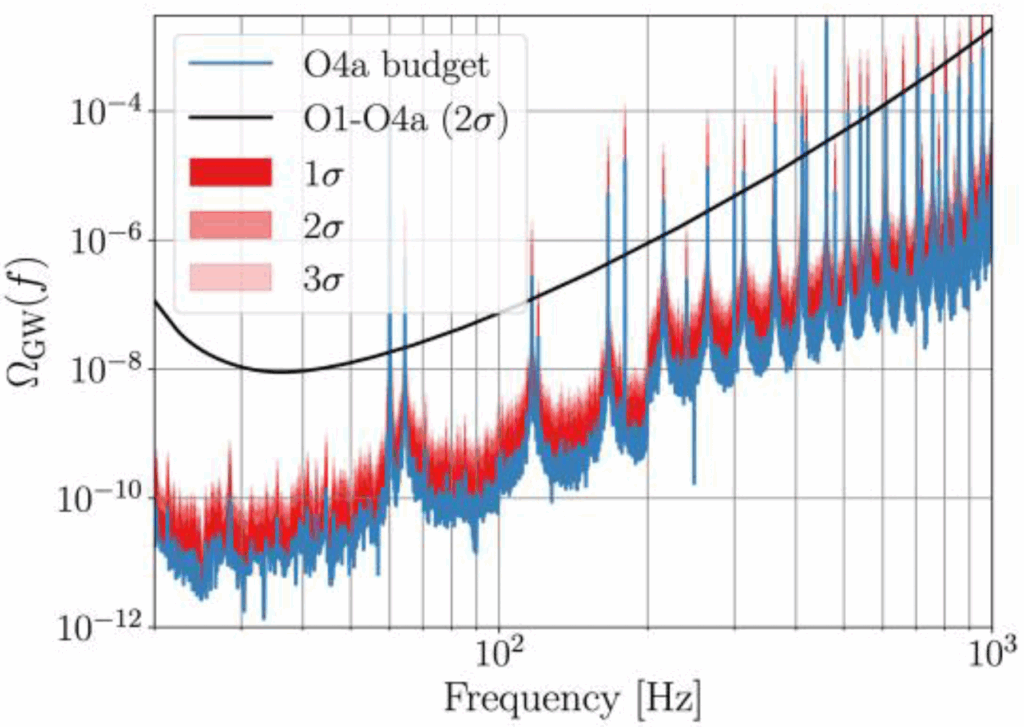
Figure 2: The effect of the correlated magnetic signal, called O4a budget (expressed in terms of the energy density of gravitational waves that would be inferred from this correlated signal in the interferometers, ΩGW). The computed magnetic budget is shown – in blue – including 1σ, 2σ, and 3σ uncertainties (in progressively lighter shades of red). The black Power–law Integrated sensitivity curve, called O1-O4a 2σ, shows the sensitivity of the search to an accumulation of magnetic noise over multiple frequency bins. We see the red band is well below this black sensitivity curve, except for narrowband features introduced by the ORF and harmonics of the 60Hz power line.
We also determined upper limits on so-called scalar or vector modes for the polarization of the SGWB that are “forbidden” polarizations in Einstein’s theory of General Relativity where only tensor polarization modes are allowed. Observing these alternative polarizations would indicate that Einstein’s theory needs to be modified. This analysis benefits from having more GW detectors to the network, since this allows the different polarizations to be better distinguished.
In our analysis we have not found evidence of these “forbidden” polarizations. Our Bayesian inference result also indicated that a tensor-polarized background (in accordance with GR) is still favored over vector, scalar, and mixed-polarized alternatives.
We finally considered our upper limits on the GWB in the context of the astrophysical background expected from merging compact binaries. We present updated estimates of energy-density spectra arising from distant binary black holes, binary neutron stars, and neutron-star black hole binaries, incorporating updated measurements of these sources’ merger rates and demographics. We found that the GWB can potentially be detected by an upgraded version of the current detectors known as LIGO A+ and Advanced Virgo Plus (see Figure 1).
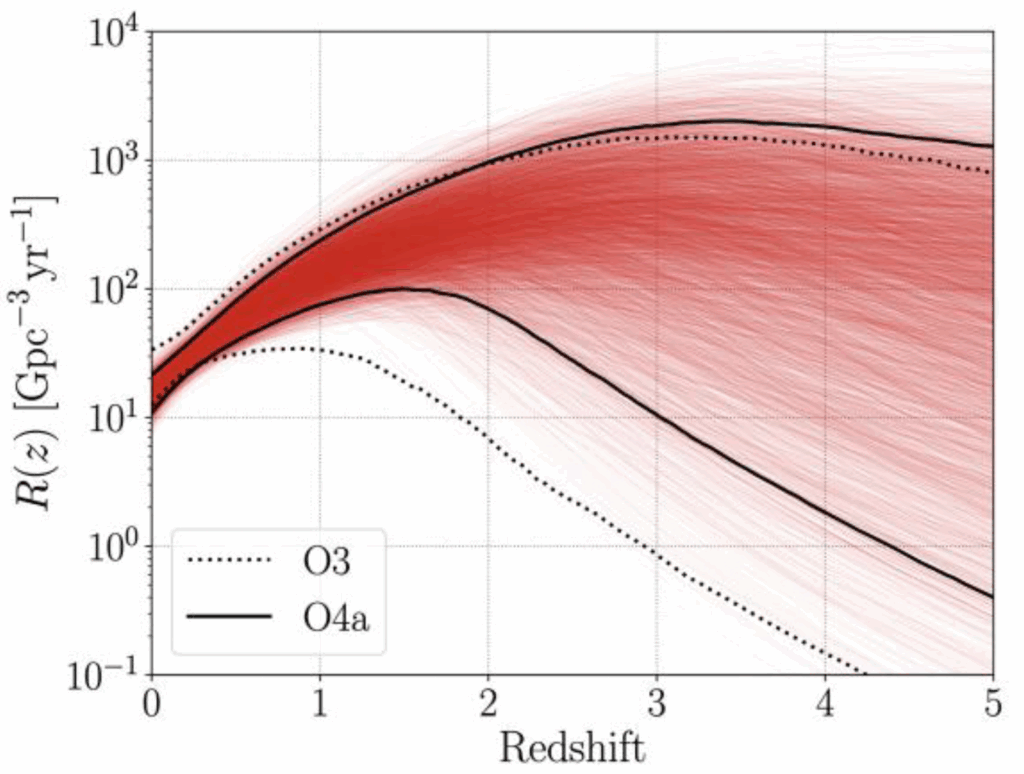
Figure 3: Inferred redshift evolution of the BBH merger rate density, measured hierarchically using the direct BBH detections in GWTC-4 and the GWB upper limit. Solid black and red lines again mark, respectively, 90% credible bounds and individual samples estimating the redshift evolution, while dotted black lines denote the 90% credible bounds obtained with our previous catalog GWTC-3.
We also applied a joint analysis to the GWB and observations of individual compact binaries from our latest published GW catalog GWTC-4. Since the GWB is sensitive to binary mergers at larger distances than the individually detectable compact binaries, it is possible that measurements of the GWB could improve measurements of the merger rate of binary black holes (BBHs) in the early universe. Here Figure 3 shows the inferred merger rate density (i.e. the number of mergers expected per unit volume of space per year) of BBHs across cosmic time inferred from combining the results of our SGWB analysis and observations of individual compact binaries from GWTC-4. For comparison, dotted black curves indicate 90% credible bounds obtained from analyzing BBH mergers in our previous catalog GWTC-3. The new results are consistent with previous estimates, although we now find that the rate with which the merger rate increases is near the upper end of the previous bounds. By adding the new data from first part of O4, our constraints on the merger rate at higher redshift have improved, though it still poorly constrained – as indicated by a wide spread of the individual samples shown as red lines in Figure 3.
Find out more:
- Visit our websites:
- Read a free preprint of the full scientific article here or on arxiv.
- Find more information on the general concept of gravitational waves here.
- Read more on the advantages of multiple detectors for gravitational-wave searches.
- Find out more about “forbidden” polarizations in general relativity.
Back to the overview of science summaries.

