Every individual detection of gravitational waves caused a ripple of excitement to pass through the collaboration — some bigger than others, it’s true — but there are some scientific results that can only be obtained by combining information from many detections together. One pair of black holes with masses a few dozen times heavier than the Sun could be a statistical outlier, but seven or eight of them together begins to look like a trend. GW150914 was the first detection of such ‘heavy stellar-mass black holes’ and came as a surprise to many, since the black holes that were previously known about in our own Galactic neighborhood were significantly smaller and lighter. However, astrophysicists soon found ways that such heavy black holes could have been produced if those stars had formed in an environment quite different from that of the Sun. In order to test such theories, the only way is to observe a larger, and maybe more varied, population of black hole events.
Over the past few years, the global network of advanced gravitational-wave detectors consisting of the LIGO and Virgo interferometers have assembled their first catalog of gravitational-wave observations. The new catalog (known as GWTC-1 or “Gravitational-wave Transient Catalog 1”), which includes signals detected over the first and second observing runs of the advanced network, reports four more binary black hole signals in addition to those already published, including the most massive binary black hole system observed to date. LIGO and Virgo have now discovered a total of 10 black hole mergers!
This growing haul of black holes is a big step towards uncovering the properties of the ‘invisible’ black hole population that permeates our Universe. We found a number of interesting aspects of the distribution, including an apparent dearth of black holes component masses prior to merger greater than 50 solar masses, preliminary constraints on the spins of these black holes, and preliminary evidence that the rate of black hole mergers increases at earlier cosmic times.
Gravitational-Wave Transient Catalog 1
During the first two observing runs of the Advanced LIGO and Advanced Virgo gravitational-wave (GW) detectors, over a year’s worth of data has been collected. The first observing run of Advanced LIGO (O1) took place from September 2015 through January 2016, and the second observing run (O2) took place from November 2016 through August 2017. During the second observing run, the Virgo interferometer also joined the search, enabling the first worldwide network of advanced GW detectors.
Ten binary black hole (BBH) mergers (as well as one binary neutron star merger) were detected during these two observing runs, and with these detections the LIGO/Virgo Collaboration has created its first catalog of GW transients. Black hole binaries are the final stage in the evolution of massive stars, and thus hold information about their progenitor star systems and the environments that led to their formation. As seen in Figure 1, the black holes detected by LIGO/Virgo already show stark differences compared to the black holes that have been indirectly inferred through electromagnetic observations.
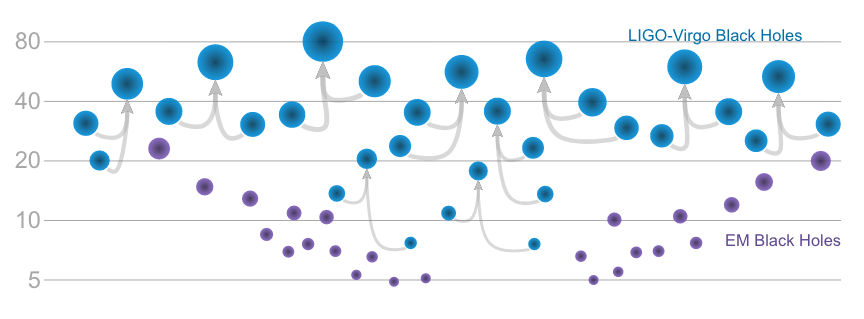
Figure 1: Masses of known black holes, both those detected by LIGO/Virgo via GWs (blue) and those indirectly observed through electromagnetic observations of X-ray binary systems (purple). The masses of the merger products are also shown. Image credit: LIGO-Virgo / Frank Elavsky / Northwestern.
What do the measured properties of BBHs detected using GWs mean with regard to the complete astrophysical BBH population? In order to present a fair assessment of our knowledge of the BBH population, we need to account for a number of subtle effects. Due to the ever-present noise background in the detectors, we cannot precisely measure the masses or spins of any merging black holes; we can only identify the most likely ‘blobs’ in the space of possible masses and spins that each merger could have — the equivalent of error bars on single measurements. Also, more massive BBH mergers in general emit louder GW signals, so can be observed at higher distances than lighter systems (something known as a Malmquist bias). Hence, we are able to see more massive binaries over a much larger volume of space. This ‘selection effect’ may partly explain why our observed mergers appear to prefer black holes with masses 30 to 40 times that of the Sun over those that are only 10 to 15 solar masses.
However, by quantifying our selection effects and measurement uncertainties, we’ve estimated how much more likely we are to find different kinds of BBHs. Using this knowledge, we can translate our observations into an estimate of the underlying population. Because we have so few observations, we must make informed guesses to fill in the gaps, a process known as Bayesian inference.
The BBH Mass Spectrum
GW measurements of black holes have already had profound implications for stellar astrophysics. Most black holes detected by LIGO/Virgo are heavier than the previously known population of stellar-mass black holes that were indirectly inferred from electromagnetic observations of X-ray binary systems; this told us something about how and where heavy BBHs might have formed. With more events, we have the opportunity to go a step further — now that we know massive stellar-mass black holes exist, can we quantify the relative rate at which different black hole masses occur in the merging population?
The “standard” mass distribution is parameterized by a power law; the probability of a black hole existing at a given mass decreases with the mass to some power: p(m) ∝ mα where α is the slope of the power law (i.e. how steeply the probability decreases with increasing mass). Using Bayesian inference and the catalog of measured masses, we can then infer the true value of the parameter in this model (α). For example, the mass distribution of heavy stars can be described by a power law with slope α = 2.3.
We examine multiple mass distribution models that have a higher degree of flexibility than the single-parameter power law and incorporate more sophisticated astrophysical predictions. For example, as opposed to assuming “fixed” minimum and maximum mass cutoffs for the power law, we allow these parameters to float and measure their values from the data. One model (Model C) has a higher degree of complexity and is described by a mixture of a power law and a Gaussian (normal) distribution. The Gaussian distribution may capture a possible build-up of black holes at higher masses (due to e.g. pulsational pair instability supernovae). The relative merger rate as a function of the primary black hole mass inferred from the catalog of BBHs is shown in Figure 2 for three different models.
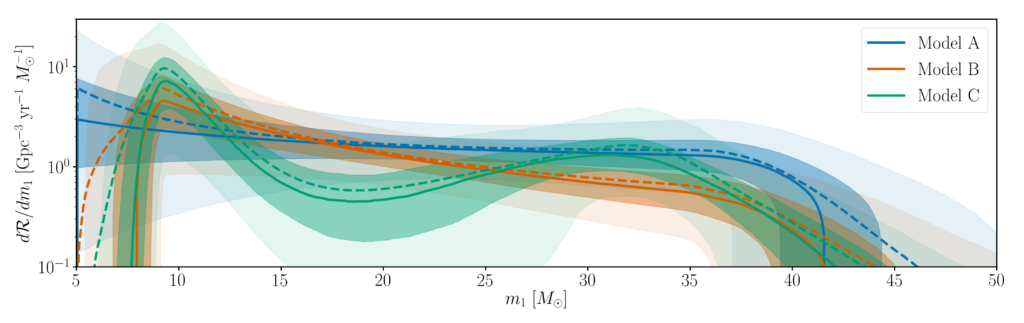
Figure 2: The number of black holes of a given mass which participate in mergers over a given volume of space, for a few different model assumptions. Model A has the least amount of complexity and Model C is the most complex. The solid lines, dark shades, and light shades show the median, 50%, and 90% credible intervals, and the dashed line shows the ‘posterior population distribution’, or best prediction for what mass a typical population member might have. Adapted from Figure 1 in the paper.
Notably, all three models find that there are almost no merging BBHs with component masses above 45 solar masses. Massive BBH mergers are detectable out to much larger cosmological distances (this is why most of our detections are more massive than black holes previously detected via X-ray emission). However, this means that if stellar-mass BBHs with component masses greater than 45 solar masses existed, we would have expected to detect some with a mass confidently in this mass range (45 solar masses to around 100 solar masses). All ten of our detected black holes are consistent with having component masses less than 45 solar masses; hence we are confident that there must be very few, if any, BBHs with more massive components. This fits in well with predictions from supernova modeling, which predict a gap in the black hole mass spectrum at around ~50 to ~130 solar masses, due to a type of supernova known as (pulsational) pair-instability supernovae. All three models agree fairly well with one another, but the model that allows for an extra Gaussian component at higher masses is slightly favored to the other two models examined, providing weak evidence that the BBH distribution deviates from a pure power law.
Spin Distributions
GW observations of coalescing compact objects also reveal information about how the compact objects are spinning — both how fast they are spinning (referred to as the spin magnitude) and how tilted the spins are relative to the orbit of the binary (referred to as spin tilt). Both pieces of information can provide unique insights about how and where the black holes formed. For example, spin magnitude measurements may reveal how different layers within massive stars interact, and spin tilts may help determine the strength of supernova explosions which form black holes, as well as whether a BBH system evolved as an isolated pair of stars or was assembled in a dense stellar environment, such as a globular cluster, through dynamical interactions between stars.
From the observations presented in the catalog, the data disfavors high spin magnitude, particularly when the individual black holes are spinning in the same direction that the binary is orbiting. Figure 3 shows the inferred spin magnitude distribution using a model where spin magnitudes are assumed to be drawn from a beta distribution. The distribution of spin tilts is somewhat less constrained (stifled in part by the low spin magnitudes, since low spin magnitudes make it difficult to disentangle the direction of the spins), and no conclusive statement can currently be made as to whether the data suggests aligned, isotropic, or a mixture of spin tilts.
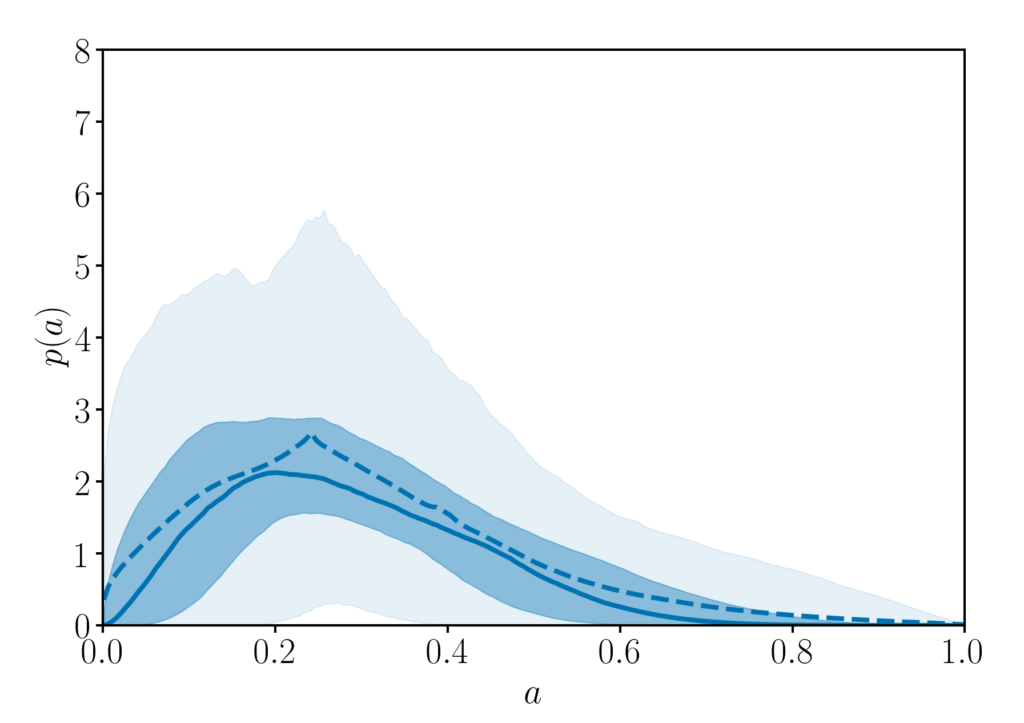
Figure 3: Inferred spin magnitude distribution for the parametric spin magnitude model used in the analysis, in units where 1 is the maximum possible spin allowed for a black hole by general relativity. The solid line, dark shade, and light shade show the median, 50%, and 90% credible intervals, and the dashed line shows the posterior population distribution. Adapted from Figure 7 in the paper.
Rate Evolution with Redshift
From this catalog of signals, one can also estimate the average number of BBH mergers per time, per volume of space as a function of redshift: ℜ(z). One naïve approximation is that this rate could be constant in comoving volume, meaning every galaxy contributes an approximately constant rate of mergers per time over cosmic history. However, the merger rate density of BBHs likely depends on other factors, such as the star formation rate as a function of redshift, which are not constant over cosmic time. To further complicate the picture, detecting a signal at a given redshift is also dependent on the intrinsic properties of that particular system such as how massive it is.
Estimates of the rate evolution are shown in blue in Figure 4. The red and yellow lines show models where the rate is assumed to be constant over cosmic time, and the mass distribution is fixed to either a power-law or flat-in-log distribution. While we can’t confidently identify a trend with redshift, our analysis does find an 88% chance that the BBH merger rate increases with redshift, meaning that in the local Universe it is likely that more BBH mergers occur at higher redshifts. This is consistent with the rate of star formation in the Universe, which was also larger at earlier cosmic times and peaks around a redshift of 2.
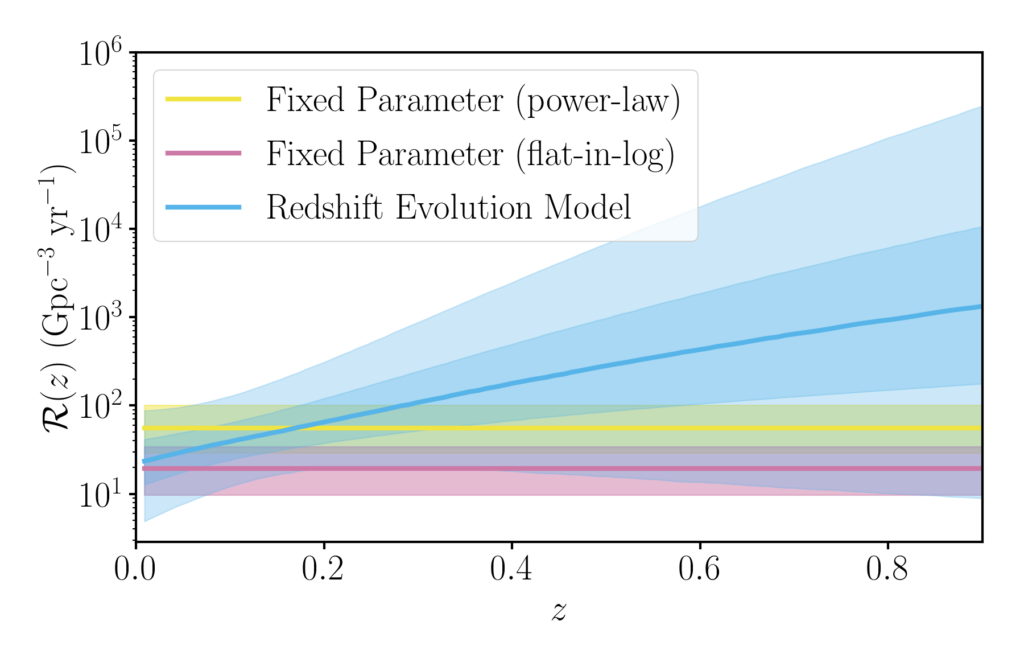
Figure 4: This plot shows the constraints on the evolution of BBH merger rate density as a function of redshift. In blue, the solid line gives the posterior median merger rate density, and dark and light bands give 50% and 90% credible intervals. Figure 5 from the paper.
Conclusions and Future Prospects
As the catalog of observed BBHs grows over the upcoming observing runs, the uncertainties in the population model parameters will shrink, and we will learn which models are preferred by the data. Among many other astrophysical quandaries, such inference can lead to a heightened knowledge of how black holes form via supernovae, how binary interactions affect massive stars, the intrinsic dynamics of dense stellar clusters, and the formation history of black holes across cosmic time.
Find out more:
- Visit our websites: https://ligo.org, http://www.virgo-gw.eu
- Read the full article, free and online here
- Read the catalog paper here
- Explore the catalog data at the Gravitational Wave Open Science Center

